はじめに
先月の中頃、2020年のQPARCの活動が無事幕を下ろしました。2021年も活発な活動を行っていくものと期待されますが、ここではこれまでのQPARC活動内容を何回かに分けてご報告したいと思います。今回はQPARC第3回~第5回基礎コース勉強会および第3回勉強会補習講座のご報告です。
第2回勉強会レポートでも述べましたが、ひとまず現在~近い将来では、量子ビット情報のエラー訂正を行わないNISQ(Noisy Intermediate-Scale Quantum device:ニスク)と呼ばれる量子コンピュータが主流となります。ただしNISQでは量子ゲート数(演算回数)が多くなるとエラーが甚大となり、有効な計算結果を得ることができません。そこで、NISQと古典コンピュータをハイブリッドに利用し、比較的少ない量子ゲート数でも計算可能なアルゴリズムが求められます。そのようなアルゴリズムの一つがVQE(Variational Quantum Eigensolver)であり、量子コンピュータ上の量子化学計算は(少なくとも当分の間)このVQEアルゴリズムを使って行われることになります。第3回~第5回勉強会では、このVQEを用いた量子化学計算の原理と実際を理解することを目標に、その理論的背景について学びました。また、第3回の学習内容の補習講座を別途行い、量子計算の基礎知識の理解を深めました。本ブログでは、その概要を簡単にまとめます。
また第3回~第5回勉強会では、量子コンピュータ上の量子化学計算を体感するために量子コンピュータシミュレータQulacsを用いた計算演習や、VQE関連の重要研究論文の解説も行われましたが、それらは紙面の都合上割愛させていただきます。VQE関連論文については本ブログの付録に記載致しましたので、ご興味のある方はそちらをご参照下さい。
第3回~第5回基礎コース勉強会のレポート
- 第3回基礎コース勉強会「量子情報の基礎」
- 開催日時:2020/7/31(金) 13:00~18:00
- 概要:量子計算のアルゴリズムを理解する上で必要な基礎知識について学びました。
- 講義内容:
- 量子計算の基礎(1)(阪大助教 御手洗光祐先生)
- 1qubit系の数式表現
- 多qubit系の数式表現
- 関連トピック(量子もつれ・量子テレポーテーション・量子ゲートの精度等)
- 量子計算の基礎(2)(QunaSys 中川裕也様)
- 量子状態(qubit)の測定
- 物理量の測定
- 物理量の期待値
- 量子計算の基礎演習(QunaSys 中川裕也様)
- 量子計算の基礎(1)(2)の内容を理解するための手計算による演習
(テンソル積・等価なゲートへの変換・物理量の一般化Pauli行列への分解・期待値の計算等)
- 量子計算の基礎(1)(2)の内容を理解するための手計算による演習
- 量子計算の基礎(1)(阪大助教 御手洗光祐先生)
- 補足・雑感:量子コンピュータの操作方法が知りたいだけのユーザにとっては、将来的にはこれらの知識はそれほど重要ではなくなるかもしれません。しかし今のところは、量子コンピュータを正しく利用するには(一般ユーザであっても)これらの内容が頭に入っている方が良いように思います。
- 第4回基礎コース勉強会「量子コンピュータ上での量子化学計算」
- 開催日時:2020/8/21(金) 13:00~18:00
- 概要:第3回の学習内容を踏まえて、量子コンピュータ上で量子化学計算を実行するための基礎知識について学びました。
- 講義内容:
- スレーター行列式と第二量子化(阪大助教 御手洗光祐先生)
- 量子化学理論の基礎(変分法・Slater行列式・Hartree-Fock法・分子軌道等)
- 第二量子化の基礎
- フェルミオン演算子から量子ビット演算子への変換(QunaSys 中川裕也様)
- Jordan-Wigner変換
- パリティ変換
- Bravyi-Kitaev変換
- スレーター行列式と第二量子化(阪大助教 御手洗光祐先生)
- 補足・雑感:この辺りのアルゴリズムは比較的良く整備されているため、実際の量子コンピュータ運用ではライブラリ関数を呼ぶだけでよく、ユーザレベルでは、変換の詳細がわからなくても計算にはさほど支障はないことが多いように思います。
- 第5回基礎コース勉強会「VQEの手法」
- 開催日時:2020/9/4(金) 13:00~18:00
- 概要:VQE法の基礎およびその応用理論について学びました。
- 講義内容:
- VQEといろいろなansatz(QunaSys 中川裕也様)
- VQEの概要・手順
- VQEのメリット・デメリット
- ansatz(試行波動関数)の選択
- 測定速度と実行時間
- 変分パラメータの最適化手法
- VQEの発展手法(QunaSys 井辺洋平様)
- ペナルティ項を用いた条件付きVQE計算手法
- VQEに基づく励起状態計算手法
- VQEエネルギーの解析的一次微分および二次微分
- VQEといろいろなansatz(QunaSys 中川裕也様)
- 補足・雑感:VQE計算にはどのような入力パラメータが必要なのか、またそれらの入力パラメータが何を意味するのかを理解することは、ユーザレベルでも重要な関心事です。特に励起状態計算では、各手法の違いをよく理解しておく必要があるように思います。またVQEエネルギーの解析的一次微分の量子計算コストが実質上ほぼゼロであることは特筆に値します。これは量子コンピュータ上での分子構造最適化が容易であることを示唆しています。
- 補習講座「量子情報の基礎」
- 開催日時:2020/9/10(木) 14:00~16:00
- 参加人数:21名(QPARC勉強会参加者数の約1/3)
- 概要:第3回での学習内容を再構成し、別の視点から量子情報の基礎知識について学びました。
- 講義内容:
(筆者が講師を担当しました。またQunaSys社の松岡様・井辺様にサポートしていただきました。)- 1qubit系の量子状態・量子ゲート
- 多qubit系の量子状態・量子ゲート
- 量子状態のベクトル表記と量子ゲートの行列表記
- qubitの測定
- 物理量の測定と期待値計算
- NISQ上での期待値計算
- 補足・雑感:後日の反応を見る限り、それなりにご好評いただけたのではないかと思います。VQE基礎理論の補習講座も計画しておりますので、ご興味のある方はぜひご参加いただければと思います(ひとまずは、QPARCメンバー限定となりますが…)。
VQEによる量子化学計算の概要
第3回~第5回勉強会で学んだVQEは、NISQ上での量子化学計算の根幹をなす重要なアルゴリズムです。そこで、VQEによる量子化学計算の感覚を皆様にもなんとなく掴み取っていただきたく、その概要や基本原理について簡単にご紹介したいと思います。
●VQEが担うのは電子相関部分
現在(古典コンピュータで)利用されている量子化学計算の9割以上は密度汎関数理論(DFT)によるものです。将来的には量子コンピュータによるDFT計算の高速化も期待されるかもしれませんが、NISQによるVQE計算の主戦場は、DFTが苦手な、電子相関が強い系となります。すなわち、DFTでは上手く求まりにくい系に対して、まず古典コンピュータ上でハートリー-フォック(HF)波動関数を計算しておき、次にHF波動関数を初期値としてVQEで電子相関の効果を求めることにより、精密なエネルギーと電子状態を得ることができます。
量子化学理論の言葉を用いれば、VQE計算は(理想的には)完全配置間相互作用(Full CI)の計算に相当します。古典コンピュータ上でのFull CI計算は、計算コストが系の大きさに対して指数関数的に増大するため、ごく小さい系でしか実現していません。しかし量子コンピュータ上ではFull CIと等価な計算がたかだか多項式オーダーのコストで実現できるため、大規模系の精密量子化学計算への期待が持たれているのです。実用的な大きさの系でのFull CI計算を近い将来に実現するのはまだ少し厳しいですが、Full CIのミニチュア版ともいえる完全活性空間(CAS)の計算なら、現在あるいは近い将来の量子コンピュータスペックでも十分実現可能であろうと思います。
●量子回路と測定
VQEの概要を述べる前に、前回ブログの復習も兼ねて、量子回路と測定のお話を少ししておきたいと思います。量子コンピュータ上の演算は、下図のような量子論理回路で表現されます。量子回路の横の線は量子ビットの流れを表しており、3個の量子ビットが左側の初期状態ψ0・ψ1・ψ2から、さまざまな量子ゲートを経て演算が行われる様子が描かれています。
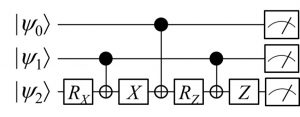
回路の最後にあたる右側のアイコンは「量子ビットの測定」を意味しています。量子コンピュータでは測定という操作により、計算結果を抽出します。ただし前回ブログでも説明しましたように、量子の世界では測定結果は確率的にしか求まりませんので、古典コンピュータのように一回の演算で答えを求めることはできません。その代わり、同じ量子回路での演算と測定を繰り返して統計を取ることで、答えの期待値を求めることができます。このことを応用すると、ある波動関数に対するハミルトニアンの期待値(=エネルギー)も求めることができるのです。(本当はこの期待値を求めるという操作もそんなに単純な話ではないのですが、ここでは演算と測定の繰り返しにより期待値が求まるという話で留めておきます。)
ところで、量子回路上の演算(量子ゲート)には、古典コンピュータにはない大きな制限があります。それは、「量子ゲートはユニタリー演算子でなければならない」という制限です。量子ビットはどんな演算が加えられようと、測定結果が0である確率と1である確率の和が必ず100%でなければなりません。したがって、量子ゲートは量子ビットのノルム(=ベクトルの長さ)が不変となるユニタリー演算子でなければならないのです。残念ながら、ハミルトニアンは一般にユニタリーではないので、このままではハミルトニアンを表現する量子ゲートを作ることができません。しかし実は、ハミルトニアンはそれぞれユニタリーなH1, H2, …の和(より正確には線形結合)の形に分解することができます。
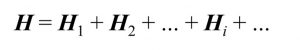
すると、H1, H2, …は量子ゲートで表現することができるため、これらの部分ハミルトニアンの期待値を計算し、最後にその和を取れば、全体のハミルトニアンの期待値が計算できることになります。
●VQEによる量子化学計算の概要
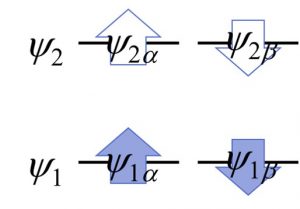
話をわかりやすくするため、最小基底での水素分子の量子化学計算を考えましょう。最小基底での水素分子は、αスピン軌道・βスピン軌道を別々にカウントすれば4個の分子軌道から成り、そのうちの2個の分子軌道に電子が1個ずつ入っています。下の図では電子が入った軌道を青色の矢印で、空の軌道を白抜きの矢印で表現しています。VQE計算ではこれらの軌道1個1個が1量子ビットに割り当てられ、各量子ビットの「1」は電子が入っている状態、「0」は電子が入っていない状態に相当します。HF波動関数では分子軌道の電子占有数は0か1しかあり得ませんが、これに電子相関の効果が加わると、非整数の電子占有が起こります。この非整数の電子占有状態、より正確に言えば、電子占有状態と電子非占有状態が重なり合った状態というのが、まさに量子ビットの性質にうってつけなのです。
VQEによる水素分子の量子化学計算の概念図を下に示します。HF波動関数の状態に初期化された量子ビットは、まず電子相関効果を表現する量子ゲートU(θ)を通過し、Ψ(θ)に変換されます。この時、U(θ)は変分パラメータθに依存することに注意して下さい。すなわち、初めのうちのU(θ)やΨ(θ)はあくまで試行的なものであり、徐々にθが最適化されていくことになります。このΨ(θ)、あるいはΨ(θ)の基となるU(θ)のことをansatz(アンザッツ)と呼ぶことが多いです。
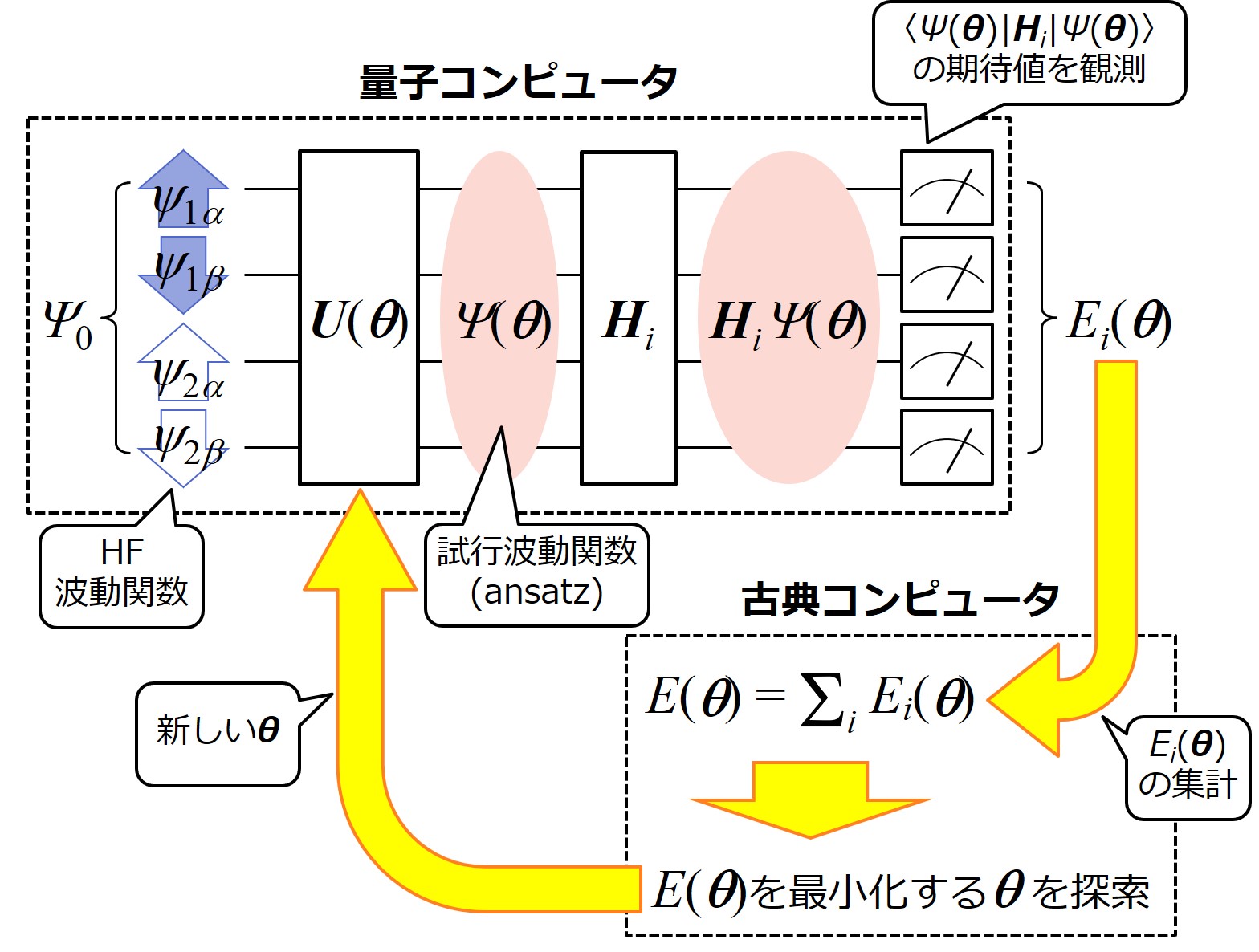
Ψ(θ)が得られたら、次にハミルトニアンを作用させて、Ψ(θ)に対するハミルトニアン期待値を求めます。ただし、前項で説明したように、ハミルトニアンの期待値を直接求めることはできないので、部分ハミルトニアンに分割して測定を行い、期待値を求めます。各部分ハミルトニアンの期待値は古典コンピュータ上で集計され、系のエネルギーE(θ)が求まります。次に、そのE(θ)を最小化するようにθが探索され、そうして得られた新しいθを量子コンピュータのU(θ)に反映させ、再びΨ(θ)のハミルトニアン期待値を求めてやります。こうして、E(θ)およびθが収束するまでこのサイクルが繰り返されます。
VQEの最重要部分は、やはり電子相関部分を担う U(θ)でしょう。このU(θ)にどのような回路を採用するかは、量子コンピュータユーザにとっても計算精度を決定する重要な関心事になると思います。ただ残念なことに、現在有効性が認められているansatzはそれほど多くなく、計算コストを考えると選択肢はさらに限られています。その中で、Symmetry-preserved ansatzはバランスの良いansatzとして注目されており、今後の研究のさらなる進展が待たれるところです。
付録:VQE関連の重要研究論文
●Calculating transition amplitudes by variational quantum eigensolvers
【論文リンク】
日本語解説: https://qunasys.com/news/2020/2/28
ポスター: https://storage.googleapis.com/qunasys/aps2020poster_gcp.pdf
【概要】三菱ケミカル社とQunaSys社の共同研究論文です。本論文ではVQEに基づく電子励起状態計算アルゴリズムを応用し、アゾベンゼンの振動子強度を計算しています。
●Elucidating reaction mechanisms on quantum computers
●Qubitization of Arbitrary Basis Quantum Chemistry Leveraging Sparsity and Low Rank Factorization
【論文リンク】

【概要】量子シミュレーションが量子コンピュータにより効率的に実行できることは R. P. Feynman により予想され、S. Lloyd によって示されました. 本論文では FeMoco を例に、2つの有望なアルゴリズムを用いて量子シミュレーションを実行する際に必要な量子コンピュータのサイズと実行時間を見積もっています。
●Accuracy and Resource Estimations for Quantum Chemistry on a Near-term Quantum Computer
【論文リンク】

【概要】For such near-term quantum computers the hybrid quantum-classical VQE algorithm in combination with the unitary coupled-cluster ansatz (UCCSD-VQE) has become an intensively discussed approach that could provide accurate results before the dawn of error-tolerant quantum computing. In this work the authors present an implementation of UCCSD-VQE that allows for the first time to treat both open- and closed-shell molecules. They study the accuracy of the obtained energies for nine small molecular systems as well as for four exemplary chemical reactions by comparing to well-established electronic structure methods like (non-unitary) coupled-cluster and density functional theory. Finally, the authors roughly estimate the required quantum hardware resources to obtain “useful” results for practical purposes.
●Ground-state energy estimation of the water molecule on a trapped-ion quantum computer
【論文リンク】

【概要】 IonQ社のイオントラップ方式の量子コンピュータを用いてVQE法を実行し、水分子の基底状態における電子相関を求めた論文です。本論文では、イオントラップ方式を活かしたエラーの少ない変分手法等や、化学精度の達成に必要な計算資源について議論されています。
●Quantum circuit learning
●Predicting excited states from ground state wavefunction by supervised quantum machine learning
【論文リンク】
(arXiv版:https://arxiv.org/abs/1803.00745)
(arXiv版:https://arxiv.org/abs/2002.12925)
【概要】NISQデバイス上の変分量子回路を用いた機械学習手法を提案した論文です。すでに引用数が150を超えており、量子機械学習を考える上で最も基礎的な論文の一つです。本論文では、ある系の基底状態の波動関数を入力データとし、その系の励起状態の性質(励起エネルギー等)を予測する量子機械学習手法を提案しています。量子機械学習におけるネックの一つである「入力データの量子状態への埋め込み」という問題を、VQEアルゴリズムの結果として得られる波動関数を用いることで自然に回避しています。



