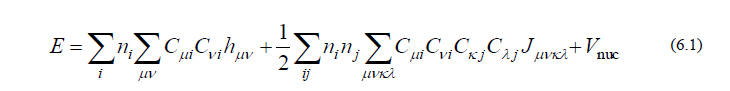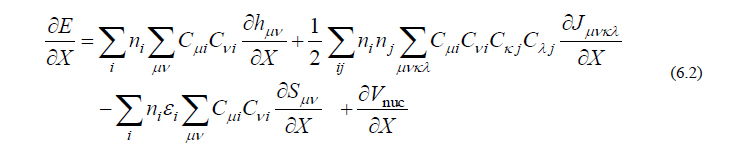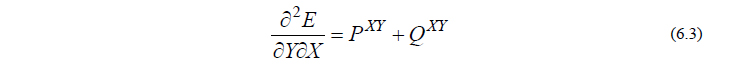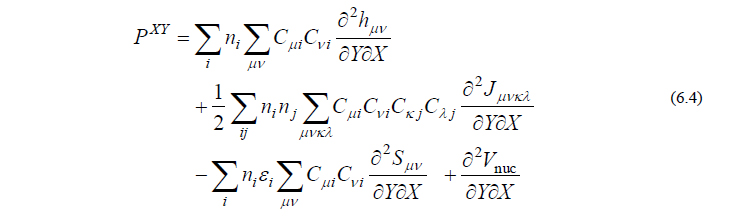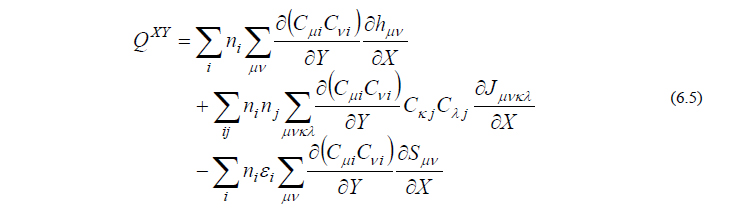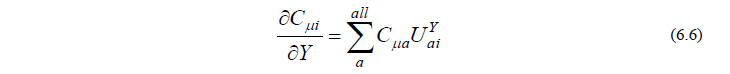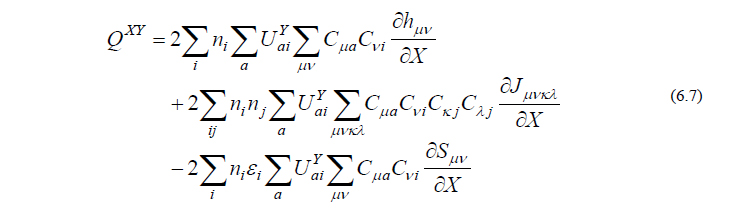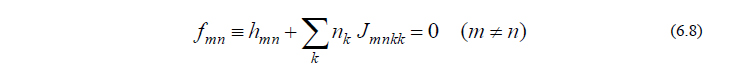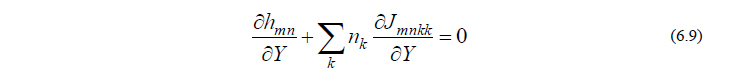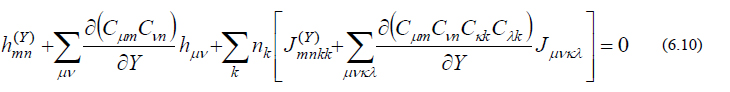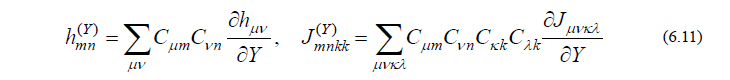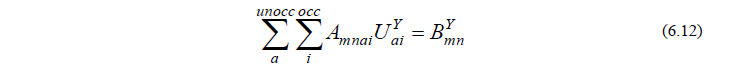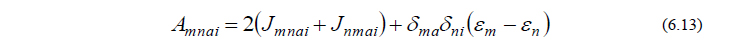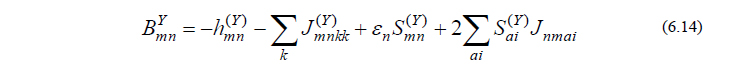Software
計算化学 ソフトウェア
Gaussian入門メールニュース:
Gaussian計算エラー対処・虎の巻
「計算がエラーで止まってしまった!でもどうすればいいかわからない。」
「結果が何かおかしい。どこがいけなかったのだろうか?」
といった疑問の解決に少しでもお力添えするべく、よくあるエラーを中心に、直接的な対処法から簡単な理論的背景まで含めて解説いたします。
第6回配信: エラーとOverlayの関係性
前回の配信では、GaussianプログラムにおけるOverlayとLinkの概念と、それらの役割について解説しました。実際のエラー対処において「どのOverlayでエラーが起こったのか」という視点は極めて有効であり、それがわかっただけで問題解決できる場合もありますし、できなくとも、より高度なエラー対処の足掛かりになると筆者は考えています。それを踏まえ、今回の配信ではエラー時のOverlayの確認方法や、各Overlayでよくあるエラーとその原因の探り方について見ていきましょう。
(6-1) OverlayとLinkの確認方法
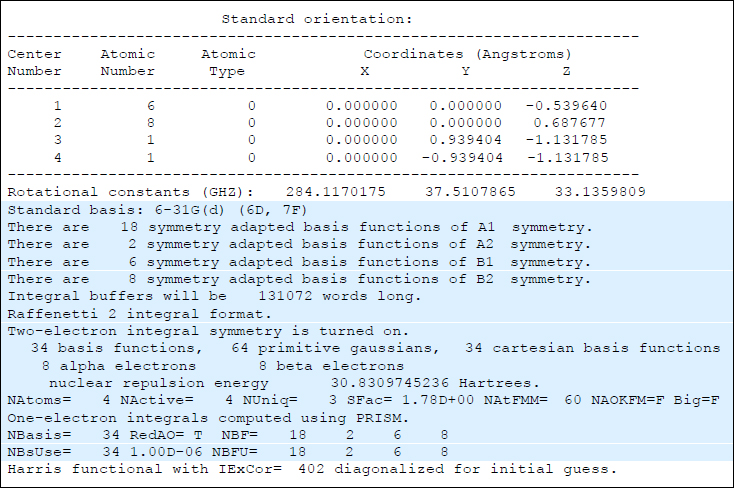
まずは「どのOverlay(Link)でエラーが起こったのか」の確認方法ですが、これを知るには通常インプットファイルで「#P」を指定しなければなりません。第1回配信で「#P」を指定する癖をつけましょうと書いたのは、主にこのためです。「#P」ではなく、通常の「#」を指定すると、以下のようなアウトプットファイル(抜粋)が得られます。
この出力情報を詳しく調べると、一番上の部分は分子座標情報ですから、OverlayでいうとOverlay 2にあたります。その次の部分は基底関数に関する情報であり、Overlay 3での出力となります。そして一番下の行は「initial guess」と書かれていますので、Overlay 4に関連した出力情報です。このように、どの出力情報がどのOverlayに相当するのかは、#P指定なしでも一応可能ですが、これを読み解くことは初心者にとって事実上不可能なことがわかります。(ここでは見やすいように、Overlay 3の出力部分に青い帯を付けましたが、当然実際のアウトプットファイルにはそのようなOverlayごとの識別サインはありません。)
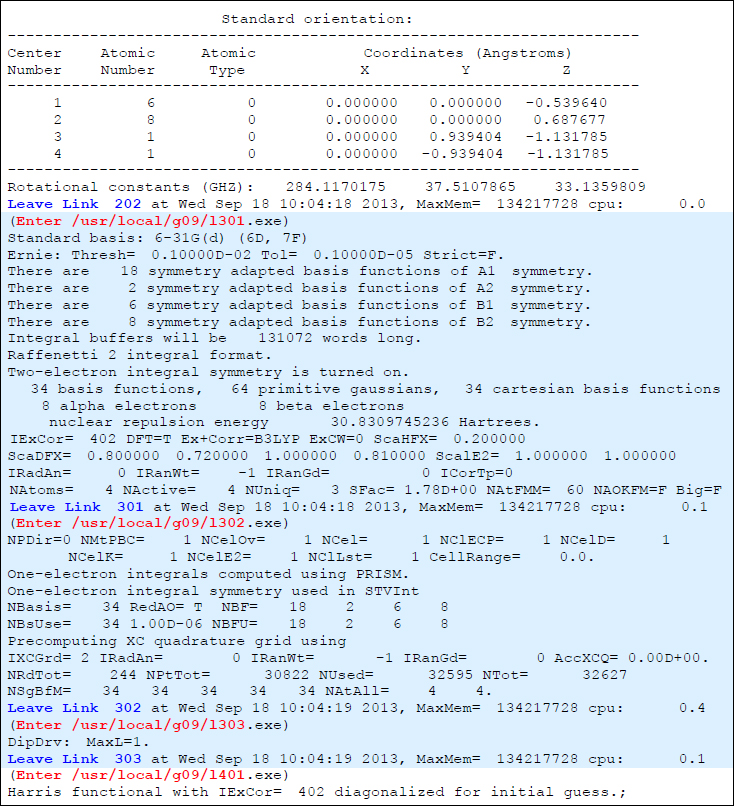
しかし、#Pを指定すると、どの瞬間にLink(あるいはOverlay)が切り替わるのかがアウトプットファイルに明確に示されます。上記の出力に相当する#P出力は、以下のようになります。
例えば、「Leave Link 202」メッセージおよび「Enter ……/l301.exe」メッセージでL202(Overlay 2) → L301(Overlay 3)の切り替わりが、「Leave Link 301」メッセージおよび「Enter ……/l302.exe」メッセージでL301 → L302の切り替わりがそれぞれ明示されており、ユーザは特別な知識がなくとも、どこからどこまでがどのLink(Overlay)なのかを知ることができます。同様に、次節で解説しますが、「どのOverlayでエラーが起こったのか」も、これらのメッセージを追っていけば容易にわかります。
(6-2) Overlayからエラー原因を探る
前回配信で述べましたように、各Overlayには固有の役割が与えられています。逆に言えば、各Overlayは与えられた役割以外の事はしないとも言えます。このことは、Gaussianのエラーの種類にはOverlayごとに特徴や上限があることを意味しており、エラーが起こったOverlayからエラーの原因究明や対処が(ある程度)可能であることを示しています。
下表に各Overlay内でよくあるエラー(赤文字は特によくありがちなエラー)をまとめました。
| Overlay | 大まかな役割 | よくあるエラー |
|---|---|---|
| Overlay 0 | 計算の開始処理 | ・Link 0コマンドの不正指定 ・キーワードの不正指定 |
| Overlay 1 | 分子構造の制御 | ・原子座標の不正指定 ・ONIOM計算入力の不正指定 ・構造最適化計算において更新後の座標が不良 |
| Overlay 2 | 対称性の制御 | ・原子座標の不正指定 |
| Overlay 3 | Fock行列に必要な項の計算 | ・基底関数の不正指定 ・電荷とスピン多重度の不整合 ・Guess=Readで、存在しないchkファイルの読み込み |
| Overlay 4 | initial guessの生成 | ・initial guessの不正指定 ・initial guessとなる軌道入れ替えの不正指定 |
| Overlay 5 | SCF収束手続き | ・SCFエネルギーの収束不良 (現象は1種類だが、根本の原因はさまざま) |
| Overlay 6 | 各種プロパティ計算 | ・NBO計算のための追加入力の不正指定 ・電子密度フィッティンググリッドの不正指定 |
| Overlay 7 | AO積分の解析的微分 | ・原子に働く力が異常に大きすぎる ・詳細振動解析のための追加入力の不正指定 |
| Overlay 8 | 2電子積分変換 | ・分子軌道凍結(積分変換領域)の不正指定 ・積分変換データによるディスク容量オーバー ・メモリ不足 |
| Overlay 9 | 電子相関計算および励起状態計算 | ・電子相関/励起状態計算パートの計算条件不正指定 ・電子相関/励起状態計算パートにおける収束異常 ・計算中間データによるディスク容量オーバー ・メモリ不足 |
| Overlay 10 | 軌道係数の解析的微分 | ・CPHF方程式解法の収束不良 ・電磁場摂動の不正指定 ・メモリ不足 |
| Overlay 11 | 軌道係数の解析的微分に必要な項の計算 | ・SAC-CI計算で、CPMOD方程式解法の収束不良 |
| Overlay 99 | 計算の終了処理 | ・構造最適化計算において分子構造が未収束 |
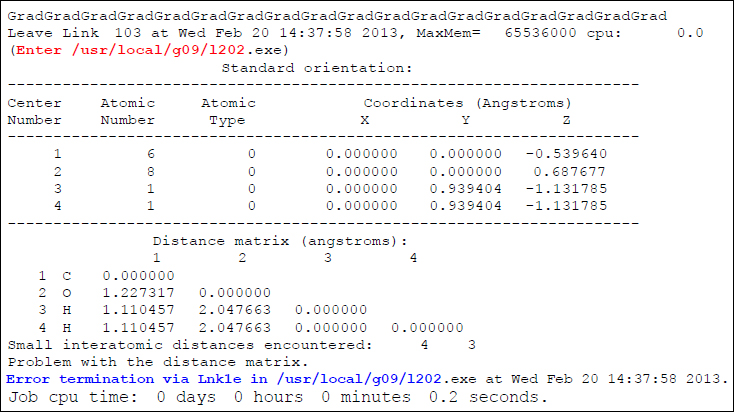
これを踏まえて、以下に例を示します。
前節のLink切り替わりメッセージや「Error termination」のメッセージから、この計算はOverlay 2(Link202)でエラー停止していることがわかります。上記の表より、Overlay 2の役割は「対称性の制御」であり、そこで起こり得るエラーは「原子座標の不定指定」であると推測されます。事実、この計算では3番目と4番目の原子座標が重なってしまっており、それがエラーの原因となっていることがわかります。(実際の場面では、4番目の原子のy座標に、本来あるべきマイナス符号を付け忘れることによって起こり得ます。)このように、エラーで停止したOverlayが把握できれば、それだけで問題解決に繋がることがあります。
しかし逆に、結果的にはあるOverlayで停止しているが、その根本の原因はそのOverlayではなく、もっと上流のOverlayにあるという可能性も常に意識しておかねばなりません。これは、あるOverlayでエラーが起きても、停止せず計算を続行することがあるからです。ただその場合も、根本の原因となるOverlayで何らかの警告的なメッセージが出力されていることが多いので、そのようなメッセージの存在に気を付けながら根気よくアウトプットファイルを見ていけば、問題解決に繋がります。
例を示しましょう。
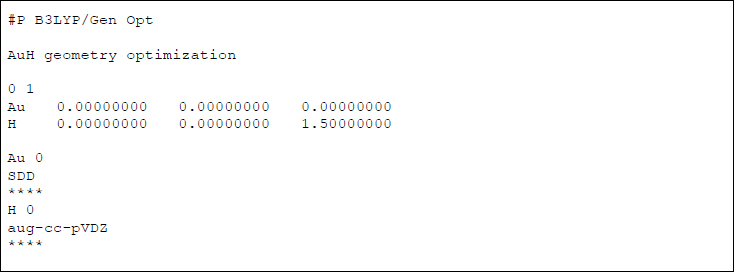
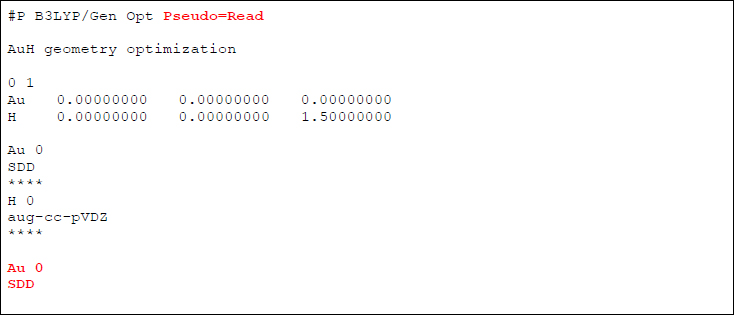
これは、Au原子にSDD基底関数、H原子にaug-cc-pVDZ基底関数を用いて、AuH分子の構造最適化を行うことを意図したインプットファイルです。重要なポイントは、SDDが重原子に対する有効内殻ポテンシャル(ECP)を含んだ基底関数だということです。ECPとは擬(pseudo)ポテンシャル法ともいい、化学現象に重要な価電子(外殻の電子)のみを顕に計算し、内殻の電子の影響は外側の電子が内側から感じるポテンシャルに置き換えてしまうという近似法です。
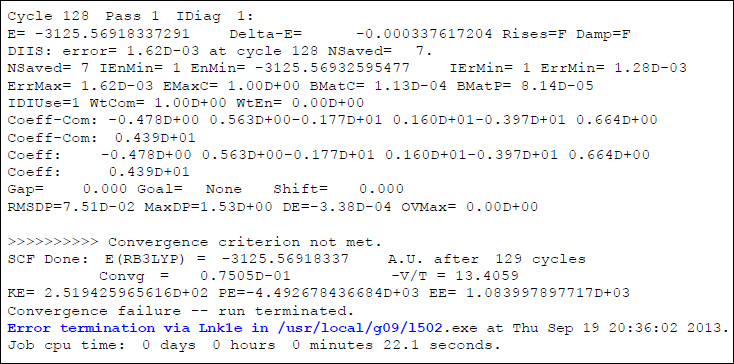
さて、このインプットで計算を行うと、以下のようなメッセージと共に計算が停止してしまいます。
エラーメッセージを見る限り、計算はL502、すなわちOverlay 5で停止していることがわかります。Overlay 5でのエラー原因は「SCFエネルギーの収束不良」ですから、一般論としては、繰り返し回数を増やしたり、収束条件を変えたりすれば、問題解決する可能性があります。しかしこの場合は、一番上の行に「Cycle 128」と出力されているように、128回ものSCF手続きを行ってもなお収束しておらず(SCF手続きの詳細に関しては第4回配信をご参照下さい)、AuHという特段に異端でもない分子で、これだけSCF手続きを行っても収束しないというのは少し変です。こういう場合は、根本の原因がOverlay 5ではなく、もっと上流のOverlayにあるため、単純に繰り返し回数上限を増やしても結果は好転しないことがほとんどです。
停止したOverlayが根本的な原因でないと予想される場合、次の方策としては2通り考えられます。1つは、アウトプットファイルを先頭から見ていき、最初に奇妙な挙動が見られるOverlayをつきとめる方法で、もう1つは、逆にアウトプットファイルの末尾から上の方へたどり、上流のOverlayでの出力情報からエラー原因を探る方法です。どちらが良いかはケースバイケースですが、筆者の場合、比較的短いアウトプットでは先頭から、長いアウトプットでは末尾からまず調べていき。最終的には両方の調査結果を照らし合わせてエラー原因を推測することが多いです。
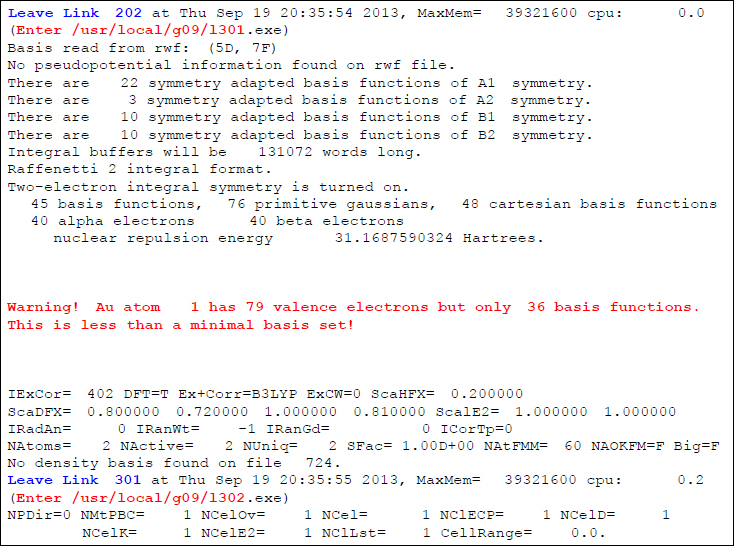
いずれの方法にせよ、この計算例のアウトプットファイルを調べていくと、以下のような出力情報を見つけることができます。
この出力情報から、L301(Overlay 3)で、基底関数に関する警告メッセージが発せられていることがわかります。警告メッセージでは「Atom 1(Au原子)は79個の電子を持っているにも関わらず、基底関数が36個しかありません。これは最小の基底関数より小さいです!」とありますが、そもそもAu原子はECPを用いて価電子のみを顕に計算するつもりですから、本来ならば79個の電子全てを顕に考慮する必要はありません。つまり、この計算のエラーの根本的な原因は、Overlay 3での基底関数の読み込みに際し、ユーザが意図したECPは採用されず、外側の価電子用の基底関数のみを用いて全電子計算しようとしていることであるということがわかります。本来計算する意図のない内殻電子を、基底関数なしで計算しようとしているわけですから、これでは計算が上手く走るはずがありません。
そこで、このメッセージを踏まえてインプットを以下のように書き換えてみます。
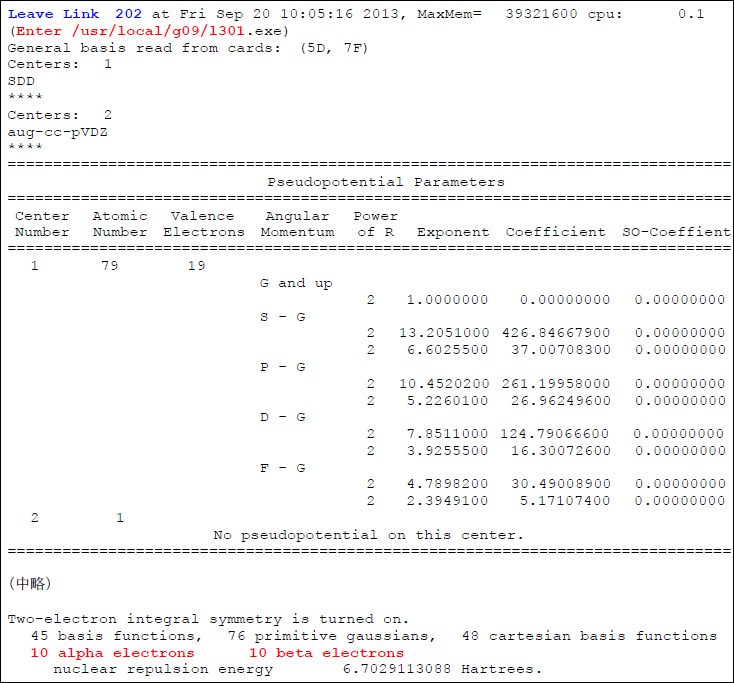
すなわち、「Pseudo=Read」キーワードで、追加入力セクションから顕に「擬(pseudo)ポテンシャルを読み込む」ように指定し、追加入力セクションで「AuにSDD擬ポテンシャルを採用する」ことを指定します。すると、
というアウトプットが得られますが、これは、AuのECPが正しく読み込まれており、かつ、顕に計算するべき電子数が計20個と、正しく内殻の電子が除外されていることを示しています。
この例では警告メッセージに顕に基底関数のことが言及されているので、そのメッセージさえ見つかれば、Overlayのことを知らなくてもエラー対処できるかもしれません。しかし「何か警告らしきメッセージがあるが、それがどういう意味なのかわかりにくい」こともしばしばあり、その場合は警告メッセージのOverlayと前節の表を参考にしながら、エラーを類推して対処していくことになるでしょう。
(6-付録) HFおよびDFT振動計算の理論的背景
ここではHF/DFT計算の分子振動計算の理論的背景をごく簡単に概説します。これまでの配信と同様、これにより第2部の配信内容の理解をより深めることができますが、あくまで付録ですので、興味のない方は読み飛ばしていただいて構いません。特に今回の内容は、難解と感じる方も多いと思いますので、理論の結果だけ知りたい方は、最後の2段落だけ読んで下さい。また、分子振動はエネルギーの原子核座標に関する2次微分で与えられますが、以下の議論はエネルギーの2次微分量であれば一般的に成り立ちますので、振動計算だけでなく、分極率、分子磁化率、核磁気共鳴などにも適用可能です。
前回の配信の通り、HF/DFT計算での分子の全エネルギーは以下のように与えられます。
また式(6.1)の原子核座標 X に関する(1次)微分表現は以下の式で与えられます。
各項の詳細は前回・前々回配信の付録に譲りますが、ここで重要な点は、式(6.1)を微分するにあたっては、厄介な軌道係数行列 C の微分は特別な方法によって回避することができ、最終的な表現が式(6.2)で表されるように C の微分を含まない形で書き表されるということです。したがって、新たに計算しなければならない微分量は、比較的容易に計算可能な h , J , S , Vnuc のみです。
さて、分子の振動を計算するには、式(6.2)を原子核座標 Y でさらに微分してやる必要があり、その表現は、以下のようになります。(なお、Y = X の場合も、以下の議論は成立します。)
ただし
ここで、PXY は軌道係数 C の微分を含まない項、QXY は C の微分を含む項を表しています。エネルギー2次微分では1次微分の時と異なり、QXY において C の微分を回避することはできず、まともに計算せねばなりません。このため、分子振動の計算は力の計算に比べて数倍程度の時間を要します。
さて、原子核座標(分子構造)をわずかに変位させると、分子軌道の形もわずかに歪みます。この歪みは、元の分子軌道が分子構造の歪みによって他の分子軌道と少しずつ混ざることによって生じたと解釈すると、実用的な計算が可能となります。そうすると、軌道係数の微分は、他の分子軌道係数の線形結合の形で書けると考えることができます。
ここで行列 UY はcoupled perturbed Hartree-Fock (CPHF)係数行列と呼ばれ、摂動 Y によって分子軌道がどのくらい混ざり合うかを表す行列です。式(6.6)を式(6.5)に代入すると、
となり、この中で未知の量はCPHF係数行列 UY だけとなります。
残りの問題は UY をどう決めるかですが、これは「Fock行列が満たすべき方程式はいかなる摂動 Y によっても不変となる」ことを利用して決定します。具体的には、(MO表現の)Fock行列が満たすべき関係式
の両辺を微分した、
という関係式を利用します。式(6.9)は「分子構造を Y によっていかに変位させようと、式(6.8)は常に満たされねばならない」ということを意味しています。式(6.9)を少し変形すると、
ただし
となりますから、詳細は省きますが、これに式(6.6)を代入して整理すると、最終的に以下のCPHF方程式と呼ばれる方程式が導かれます。
ただし
A は既知の2電子積分より、BY は既知の1電子積分・2電子積分およびそれらの微分によりそれぞれ計算される行列であり、いずれも容易に計算することができる量です。CPHF方程式(6.12)は連立一次方程式の形をしており、これを解くことによって UY が得られます。これで、最終的に得たい量(6.3)を計算するために必要な量全てが揃ったことになります。
ここで、エネルギー2次微分に関する以上の流れをまとめ、GaussianでのOverlayとの関係性について考えてみたいと思います(実際のGaussianプログラムでは、効率的な計算を行うため、必ずしも以下の流れに沿っているわけではありませんが、本質的には差し支えありません)。振動計算を行うためには、式(6.3)、すなわち、PXY と QXY の計算が必要ですが、このうち QXY を求めるにはCPHF方程式(6.12)を解かねばなりません。さらに方程式(6.12)を解くためには、式(6.13)、(6.14)を計算して行列 A と BY を用意してやる必要があります。この A と BY の計算をOverlay 11で行います。次に、A と BY が求まったら、CPHF方程式(6.12)を解く作業をOverlay 10で行います。そして、この方程式を解いてCPHF係数 UY が求まったら、PXY と QXY の計算が可能となりますので、それをOverlay 7で行います。
前回配信では、話が難しくなることを避けるために、微分計算パート(Overlay7、10、11)の役割についてほとんど触れませんでしたが、実際の振動計算アウトプットファイルからOverlayの流れを読み取ると、大抵Overlay 11→10→7という流れを含んでいることが読み取れます。これは上記の内容と一いたしていることがわかります。また、MP2、CCSD、SAC/SAC-CIなどの電子相関計算の構造最適化計算では、(1次微分であっても)顕に軌道係数の微分を行わねばならないため、同様なOverlayの流れとなります。一方、単なるHF/DFT構造最適化計算の場合は、軌道係数の微分が回避できますから、CPHF方程式を解く必要はありません。そのため、(前回配信の付録でも触れたように)1電子積分と2電子積分の微分を行うOverlay 7までが呼び出され、CPHF方程式に関係するOverlay 10、11は呼び出されません。
今回の内容は以上です。また「第2部 Gaussianでエラーが起こる仕組みを知る」もこれにて終了し、次回からは「第3部 Gaussianエラー対処各論」に入ります。次回(第7回配信)では、「Link 0コマンド指定に関するエラー」を解説いたします。
メールニュース会員募集中!
Gaussian入門者の皆様に、Gaussianを使いこなして高度な計算化学者に飛躍していただけるよう、Gaussianに関する様々な情報を発信しております。メールニュースの配信をご希望の方は、以下のフォームよりお願いいたします(お問い合わせ内容の項に「Gaussian入門メールニュース配信希望」とご記入ください)。
メールにてお申し込みされる方は、以下の必要事項をご記入の上、送信してください。
- ◆電子メール件名 : Gaussian入門メールニュース配信希望
- ◆記入項目:
1. 氏名 :
2. E-mail:
3. 法人名/部署名:
4. 住所:
5. 電話番号:
お問い合わせ
平日9:30~17:30 (土曜日、日曜日、祝祭日、年末年始、夏期休暇は、休日とさせていただきます。)