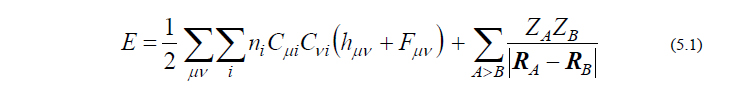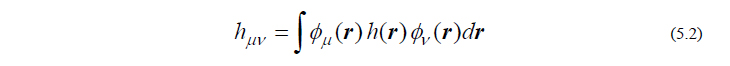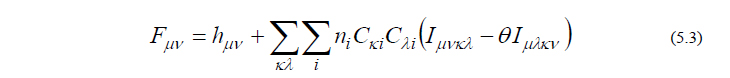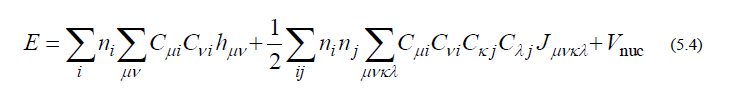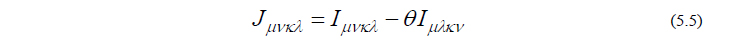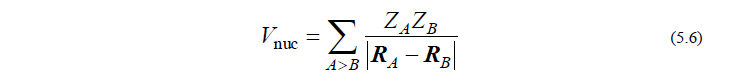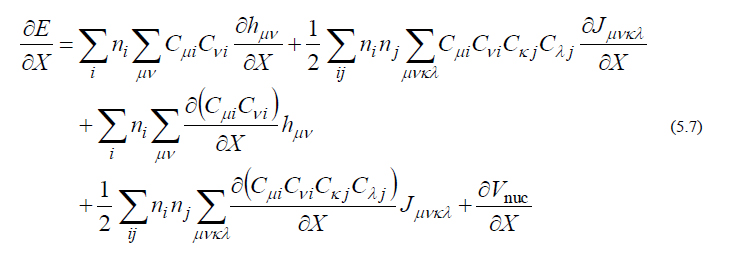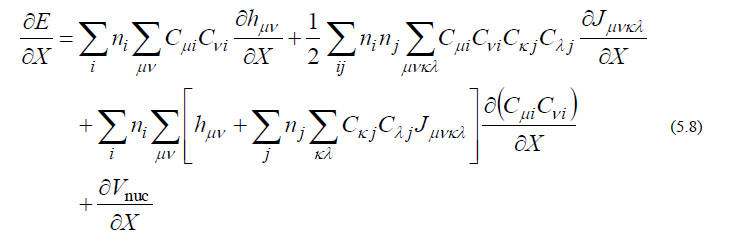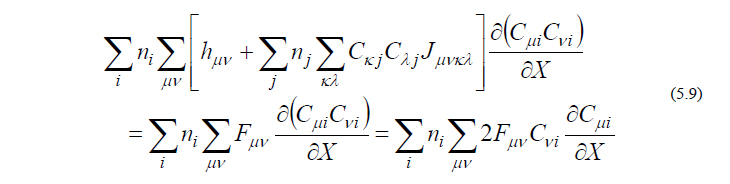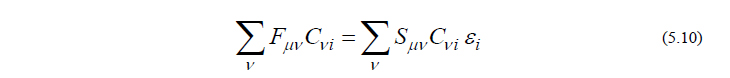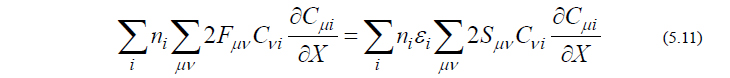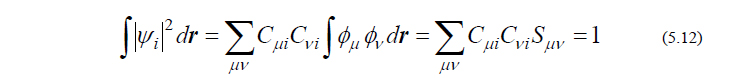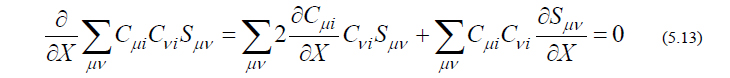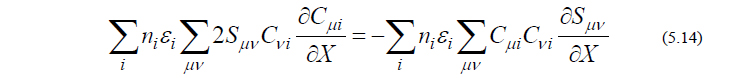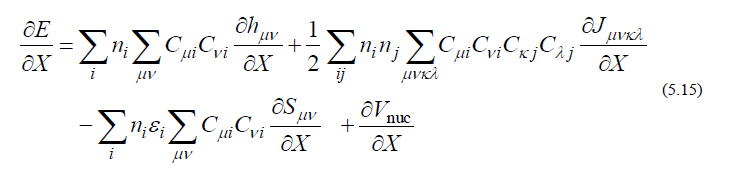Software
計算化学 ソフトウェア
Gaussian入門メールニュース:
Gaussian計算エラー対処・虎の巻
「計算がエラーで止まってしまった!でもどうすればいいかわからない。」
「結果が何かおかしい。どこがいけなかったのだろうか?」
といった疑問の解決に少しでもお力添えするべく、よくあるエラーを中心に、直接的な対処法から簡単な理論的背景まで含めて解説いたします。
第5回配信: Gaussian計算の流れ
前回の配信ではGaussianでエラーが起こる理屈を理解するために一般的な量子化学計算の流れについて解説しました。それを踏まえて今回は、実際のGaussianプログラムではどのような流れに沿って計算が走るのかを見ていきましょう。
(5-1) Overlayの概念
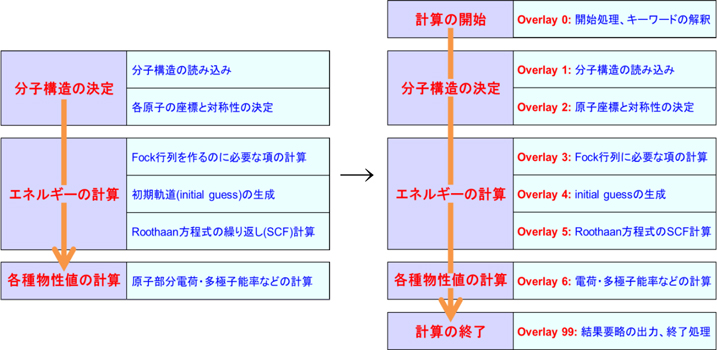
単純のために、HF/DFT一点計算の場合を考えましょう。前回の配信でお話しした通り、この計算は下の左図のように6個のプロセスに分割され、それらのプロセスの連なりとして表されます。このようにプロセス単位で考えることは、計算が不首尾に終わった場合、どこに失敗の原因があったかが明確になるというメリットがあることを学びました。Gaussianでは、これらの「プロセス」のことを「Overlay」と呼びます。このOverlayの概念を使って左図を書き直すと、右図のようになります。
各プロセスはOverlay 1~Overlay 6という固有の名前で呼ばれ、それらの前後にOverlay 0、Overlay 99という特別なOverlayが置かれます。Overlay 0は計算の開始処理、Overlay 99は計算の終了処理を司るプロセスであり、全てのGaussian計算は、必ずOverlay 0から始まって、Overlay 99で終わります。
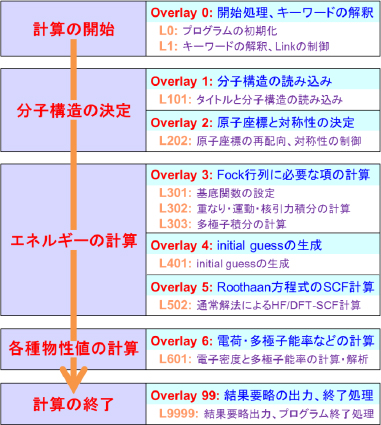
上のHF/DFT一点計算の例では(Overlay 99を除くと)Overlay 6までしか登場しませんが、Gaussian には全部で13個のOverlayが存在し、以下の表のように、Overlayごとに大まかな役割を分担させています。
| Overlay | 大まかな役割 | 主な具体的処理 | 関連Link(後述) |
|---|---|---|---|
| Overlay 0 | 計算の開始処理 | ・プログラムの初期化 ・キーワードの解釈 ・ジョブストリームの決定 | L0, L1 |
| Overlay 1 | 分子構造の制御 | ・原子座標の読み込み ・原子座標の更新 ・エネルギー数値微分のための制御 ・ONIOM計算の制御 | L101, L102, L103, L105, L106, L107, L108, L109, L110, L111, L112, L113, L114, L115, L116, L117, L118, L120, L121, L122, L123, L124 |
| Overlay 2 | 対称性の制御 | ・原子座標の再配向とチェック ・対称性の制御 | L202 |
| Overlay 3 | Fock行列に必要な項の計算 | ・基底関数の設定 ・1電子AO積分の計算 ・2電子AO積分の計算 | L301, L302, L303, L308, L310, L311, L314, L316, L319 |
| Overlay 4 | initial guessの生成 | ・initial guessの生成 | L401, L402, L405 |
| Overlay 5 | SCF収束手続き | ・分子軌道のSCF収束手続き ・SCF分子軌道の決定 | L502, L503, L506, L508, L510 |
| Overlay 6 | 各種プロパティ計算 | ・SCF分子軌道の解析 ・atomic charge、多極子モーメントの計算 ・NBO解析 | L601, L602, L604, L607, L608, L609, L610 |
| Overlay 7 | AO積分の解析的微分 | ・1電子AO積分の解析的微分計算 ・2電子AO積分の解析的微分計算 | L701, L702, L703, L716 |
| Overlay 8 | 2電子積分変換 | ・電子相関計算および励起状態計算のための 2電子AO→MO積分変換 | L801, L802, L804, L811 |
| Overlay 9 | 電子相関計算および 励起状態計算 | ・TD-DFT ・CIS、CIS(D)、CID、CISD ・MP2、MP3、MP4、MP5 ・CCSD、CCSD(T) ・SAC/SAC-CI | L901, L902, L903, L904, L905, L906, L908, L913, L914, L915, L916, L918, L923 |
| Overlay 10 | 軌道係数の解析的微分 | ・CPHF方程式の構築と実行 ・CISの解析的2次微分計算 | L1002, L1003, L1014 |
| Overlay 11 | 軌道係数の解析的微分に 必要な項の計算 | ・高次微分に必要な積分の微分計算 ・2粒子密度行列の微分計算 ・MP2の2次微分計算 | L1101, L1102, L1110, L1111, L1112 |
| Overlay 99 | 計算の終了処理 | ・計算結果のまとめの出力 ・プログラムの終了処理 | L9999 |
計算中間結果は、Overlay 1からOverlay 2、Overlay 2からOverlay 3へと次々に引き渡されていきます。中間結果がどのOverlayをどのように通っていくかのことを「ジョブストリーム」と言い、これはOverlay 0内で決定されます。このジョブストリームは、アウトプットファイルからも確認することができます。例えば、DFTの一点計算の場合、アウトプットファイルの冒頭付近に以下のような出力を見ることができます。
今は、各行の一番左の数字だけに注目して下さい。すると、1→2→3→4→5→6→99という数字の並びになっており、これはこの節の初めに説明したOverlayの流れの図に一いたしていることがわかります。
同様にTD-DFTの一点計算の場合を見てみると、
Overlay の流れは1→2→3→4→5→8→9→6→99であり、基底状態DFT 計算で通るOverlayに加えて、Overlay 8とOverlay 9を通っています。これらのOverlayの役割を先ほどの表から調べると、Overlay 8は励起状態計算の前処理として必要な2電子積分変換、Overlay 9は実際の励起状態の計算をそれぞれ担っていることがわかります。一方、このジョブストリームに採用されていないOverlay 7、10、11は全て微分計算に関係するOverlayであり、エネルギーの微分を行わない一点計算の場合にはこれらのOverlayは関係ありません。したがって、このジョブストリームは励起状態の一点計算に必要十分なOverlay構成として理にかなっていることがわかります。
さて、さまざまなエラーに対処していくには、そのエラーが起こる理屈から理解する必要があると以前の配信でも述べてきましたが、これをGaussian計算の場合で言い換えれば、どのOverlayでどのようなエラーが起こったのかを理解することが重要であると筆者は考えています。もちろん、それを理解しただけでは解決できない、もっと深い知見が必要となる問題があることも事実です。しかし、エラーが起こったOverlayが把握できれば、それだけですぐに問題解決できる場合もありますし、さらに、そのOverlayが計算全体の流れの中でどういう役割や処理を担っているかを大雑把にでも知っていれば、エラー原因の考察がぐっと楽になります。次回配信では、エラー時のOverlayの確認方法や、各Overlayで起こり得る典型的なエラーについて解説する予定です。
(5-2) Linkの概念
Gaussian計算はOverlayというプロセスの連続により制御されており、その流れの中で各Overlayは任せられた役割を果たすために具体的な処理を行うのですが、その処理内容は前節の表からもわかるように大抵1つではなく、幾つかの「小プロセス」に分割して考えた方が便利なことが多いです。これは、ハンバーグの調理の例で言えば、「食材の下ごしらえ」というプロセスが、実際には「材料を適切な大きさに切る」「切った玉ねぎを炒める」「パン粉に水を加えて絞る」などといった幾つかの「小プロセス」から構成されることと似ています。この、Overlayを構成する「小プロセス」のことをGaussianでは「Link」と呼びます。
計算中間結果はOverlayからOverlayへ引き渡されますが、各Overlay内では、そのOverlayを構成するLinkからLinkへと引き渡されます。例えば、HF/DFT一点計算の場合、その流れは以下のようになります。
すなわち、Linkの流れとしては、0→1→101→202→301→302→303→401→502→601→9999となります。また全てのGaussian計算は、必ずLink 0から始まって、Link 9999で終わります。
Overlayと同様に、その計算におけるLinkの流れも、アウトプットファイルからも確認することができます。再び、DFTの一点計算の場合を例に挙げましょう。
今度は(2つのスラッシュ間の内容✝は無視して)左端と右端の数字に注目して下さい。すると、
となり、これは実際のLink の流れ、(0→1→)101→202→301→302→303→401→502→601→9999 に一いたしていることが分かります。
各Linkとその役割を下表に示します。ただ、エラー対策という目的ではLinkの役割までしっかり勉強する必要はなく、大抵は前節のOverlayの役割が大まかに把握できていれば十分です。下表は、Overlayより細かいLinkの役割にまで踏み込んでエラー原因を考察する必要がある場合に、辞書的にご利用下さい。
| Overlay | Link | 主な役割 |
|---|---|---|
| Overlay 0 | L0 | プログラムの初期化、Overlayの制御 |
| L1 | キーワードの解釈、実行Linkリストの構築、スクラッチファイルの初期化 | |
| Overlay 1 | L101 | タイトルと分子指定の読み込み |
| L102 | Fletcher-Powell法による構造最適化 | |
| L103 | Berny法による構造最適化(最安定構造、遷移状態構造、STQN遷移状態構造) | |
| L105 | Murtaugh-Sargent法による構造最適化 | |
| L106 | 分極率・超分極率を求めるための力・双極子の数値微分計算 | |
| L107 | 線形同時通過(LST)法による遷移状態構造の探索 | |
| L108 | 非緩和ポテンシャルエネルギー曲面の走査 | |
| L109 | Newton-Raphson法による構造最適化 | |
| L110 | エネルギーの数値的2次微分による分子振動計算 | |
| L111 | エネルギーの数値的2次微分による分極率・超分極率の計算 | |
| L112 | self-consistent virial scaling(SCVS)法の実行 | |
| L113 | 解析的微分を用いた固有値追従(EF)アルゴリズムによる構造最適化 | |
| L114 | EFアルゴリズムによる数値的構造最適化(エネルギーのみを使用) | |
| L115 | GS3アルゴリズムを用いた反応経路追跡 | |
| L116 | 自己無撞着反応場(SCRF)の数値的計算 | |
| L117 | 等電子密度面分極連続体モデル(IPCM)による溶媒和計算 | |
| L118 | Born-Oppenheimer分子動力学(BOMD)計算 | |
| L120 | ONIOM計算の制御 | |
| L121 | 原子中心密度行列伝播(ADMP)分子動力学計算 | |
| L122 | Counterpoise(CP)補正計算 | |
| L123 | Hessian-based Predictor-Corrector(HPC)アルゴリズム等を用いた反応経路追跡 | |
| L124 | PCM付きONIOMおよび外部反復PCMの計算 | |
| Overlay 2 | L202 | 原子座標の再配向、対称性の制御、変数のチェック |
| Overlay 3 | L301 | 基底関数情報の生成 |
| L302 | 重なり積分、運動エネルギー積分、核-電子引力ポテンシャル積分の計算 | |
| L303 | 多極子積分の計算 | |
| L308 | 双極子速度( ∇ )および角運動量( R × ∇ )積分の計算 | |
| L310 | 非短縮様式でのspdf 2電子積分の計算 | |
| L311 | sp 2電子積分の計算 | |
| L314 | spdf 2電子積分の計算 | |
| L316 | 2電子積分の出力 | |
| L319 | 近似的スピン-軌道相互作用に関する1電子積分の計算 | |
| Overlay 4 | L401 | 分子軌道のinitial guess生成 |
| L402 | 半経験的計算および分子力学(MM)計算 | |
| L405 | 多配置(MC)-SCF計算の初期化 | |
| Overlay 5 | L502 | SCF方程式の反復的解法(従来法、all direct法、SCRF計算) |
| L503 | 直接最小化を用いたSCF方程式の反復的解法 | |
| L506 | ROHFまたはGVB-PP計算 | |
| L508 | 2次収束SCFプログラム | |
| L510 | MC-SCF計算 | |
| Overlay 6 | L601 | 電荷密度および関連量の解析(多極子モーメントの計算を含む) |
| L602 | 1電子プロパティの計算(ポテンシャル、電場、電場勾配など) | |
| L604 | グリッド点上の分子軌道および電子密度の評価 | |
| L607 | 自然結合軌道(NBO)解析 | |
| L608 | 非反復的DFTエネルギーの計算 | |
| L609 | Atoms in Molecules(AIM)プログラム | |
| L610 | 数値的積分(積分プログラムのテスト用) | |
| Overlay 7 | L701 | 1電子積分の1階および2階微分計算 |
| L702 | 2電子積分の1階および2階微分計算(sp関数) | |
| L703 | 2電子積分の1階および2階微分計算(spdf関数) | |
| L716 | 構造最適化および振動計算用の情報処理 | |
| Overlay 8 | L801 | 2電子積分変換の初期化 |
| L802 | 積分変換の実行(N 3 in-coreアルゴリズム) | |
| L804 | 積分変換の実行 | |
| L811 | 積分導関数変換およびそれらのMP2の2次微分への寄与の計算 | |
| Overlay 9 | L901 | 2電子積分の反対称化 |
| L902 | Hartree-Fock波動関数安定性の決定 | |
| L903 | 旧アルゴリズムのin-core MP2計算 | |
| L904 | Peterssonらの方法による完全基底系(CBS)外挿 | |
| L905 | 複素数MP2計算 | |
| L906 | semi-directアルゴリズムMP2計算 | |
| L908 | 電子伝播関数プログラム | |
| L913 | post-SCF(電子相関)エネルギーとその微分計算 | |
| L914 | CI-Single計算、乱雑位相近似(RPA)計算、ZIndo励起状態、SCF安定性 | |
| L915 | MP5、QCISD(TQ)、BD(TQ)における5次量の計算 | |
| L916 | 旧アルゴリズムのMP4およびCCSD計算 | |
| L918 | 波動関数の再最適化 | |
| L923 | SAC/SAC-CI計算 | |
| Overlay 10 | L1002 | CPHF方程式の反復的解法(NMR計算を含む) |
| L1003 | CP-MCSCF方程式の反復的解法 | |
| L1014 | CI-Singleの解析的2次微分計算 | |
| Overlay 11 | L1101 | 1電子積分導関数の計算 |
| L1102 | 双極子導関数積分の計算 | |
| L1110 | F (x) に対する2電子積分の微分項の寄与 | |
| L1111 | 2粒子密度行列と電子相関項の微分計算 | |
| L1112 | MP2の2次微分計算 | |
| Overlay 99 | L9999 | 計算結果のまとめの出力、プログラムとアウトプットの終了処理 |
(5-付録) HFおよびDFT構造最適化計算の理論的背景
ここではHF/DFT計算の構造最適化計算の理論的背景をごく簡単に概説します。前回配信と同様、これにより第2部の配信内容の理解をより深めることができますが、あくまで付録ですので興味のない方は読み飛ばしていただいて構いません。
前回配信の通り、分子の全エネルギーは以下のように与えられます。
ここで、ギリシャ文字、小文字アルファベット、大文字アルファベットのindexはそれぞれ基底関数、分子軌道、(分子を構成する)原子のindexを意味し、Cμi は分子軌道係数、ni は i 番目の分子軌道の占有電子数、ZA は原子Aの核電荷、RA は原子Aの座標ベクトルを表します。残りの hμv , Fμv は1電子ハミルトニアン行列、Fock行列と呼ばれ、それぞれ
で与えられます(各項の意味は前回配信の付録をご参照下さい)。以上の量はRoothaan方程式を解けば全て求まり、Overlay 5が終了した時点で既知情報となります。
さて、分子の構造最適化を行う場合、各原子(核)に働く力を計算し、その力のベクトルの方向に原子を動かしてやらねばなりません。そのためには、式(5.1)を各原子(核)座標で微分した表現を得る必要があります。まず、式(5.1)の形を少し簡略化して書き直しておきます。
ただし、
式(5.4)をある原子(核)座標 X について微分すると、
となります。この式(5.7)の第1項、第2項、第5項の微分計算は比較的簡単にできるのですが、第3項、第4項は分子軌道係数の微分を含んでおり、まともに計算するのはかなり厄介です。というのも、分子軌道係数の数式はRoothaan方程式を介した陰な形でしか与えることができず、陽な数式の形で書き表すことができないからです。しかし、HF/DFTエネルギーの1次微分の場合に限り、この問題は回避することができます。式(5.7)をさらに変形すると、以下の式を得ます。
ところが、[ ] の中身を式(5.3)と見比べると、これはFock行列そのものであることがわかります。すると、
であり、さらにこれをRoothaan方程式
と比較すると、以下の表現を得ます。
ここで、分子軌道の規格化条件より、
であり、これを微分すると、
となり、式(5.11)と式(5.13)を見比べることにより、以下の関係式が得られます。
この式(5.14)は、厄介な軌道係数の微分が、わずかな計算量で済む重なり積分の微分にすり替えられるという点において、極めて重要な意味を持ちます。
以上をまとめると、HF/DFTエネルギーの微分表現は、最終的に以下の式で与えられます。
式(5.15)において新たに計算しなければならないのは h , J , S , Vnuc の微分量ですから、その計算を行えば、各原子(核)に働く力を求めることができます。Gaussianではこの操作をOverlay 7で行っています。
力が求まったら、そのベクトルの方向へ実際に原子(核)を動かしますが、これはGaussianではOverlay 1に戻って行います(Overlay 7では、力を求めるところまで)。Gaussianでは力の大きさと、どれだけ原子を動かしたかを収束判定条件に採用しており、収束と見做されれば必要な出力の後に計算が終了し、未収束と見做されればOverlay 1~7の手順が再度繰り返されます。
一方、2次以上のエネルギー微分(分子振動、分極率、分子磁化率、核磁気共鳴などの計算に必要)や、電子相関理論(MP2、CCSD、SAC/SAC-CIなど)のエネルギー微分の計算では、分子軌道係数の微分はもはや避けることができません。軌道係数の微分を行うには、Coupled Perturbed Hartree-Fock(CPHF)方程式という連立方程式を新たに解く必要があります。これについては、次回配信の付録にて解説する予定です。
✝ ジョブストリーム情報における2つのスラッシュ間の文字列は、「IOp形式」と呼ばれる形式で指定された計算条件を表します。
IOp形式は、Gaussianキーワードに用意されていないような細かい計算条件の指定をする時に、主に用いられます。
IOp形式に関する詳細は、Gaussian社公式ユーザマニュアルおよびGaussian社公式IOpマニュアルをご参照下さい。
今回の内容は以上です。次回(第6回配信)では、「エラーとOverlayの関係性」を解説いたします。
メールニュース会員募集中!
Gaussian入門者の皆様に、Gaussianを使いこなして高度な計算化学者に飛躍していただけるよう、Gaussianに関する様々な情報を発信しております。メールニュースの配信をご希望の方は、以下のフォームよりお願いいたします(お問い合わせ内容の項に「Gaussian入門メールニュース配信希望」とご記入ください)。
メールにてお申し込みされる方は、以下の必要事項をご記入の上、送信してください。
- ◆電子メール件名 : Gaussian入門メールニュース配信希望
- ◆記入項目:
1. 氏名 :
2. E-mail:
3. 法人名/部署名:
4. 住所:
5. 電話番号:
お問い合わせ
平日9:30~17:30 (土曜日、日曜日、祝祭日、年末年始、夏期休暇は、休日とさせていただきます。)