Software
計算化学
量子化学の基礎知識
1. 量子化学のシミュレーションモデル
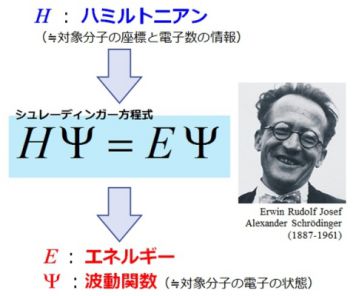
量子化学では、(通常の化学の範囲内で)物質の構成最小要素である原子核や電子を取り扱うSchrödinger方程式(下式)を、可能な限り精密に解くことに基づいている。
ここで、Hはハミルトニアン、Ψは波動関数と呼ばれる。Hは、対象系の分子構造や電子数などの情報を含んでおり、この方程式のいわばインプット情報になる。答えとなるアウトプット情報は、EとΨであり、それぞれ系のエネルギーと電子状態を表している。したがって、この方程式を精密に解くことにより(原理的には)分子構造と電子数の情報を与えるだけで、実験結果に迫る精度で計算結果が得られることになる。
分子が時間的に構造変化する問題は(原理的には取扱可能だが)実際の計算が困難であるため、対象系は真空中・絶対零度の静止分子に限定され、分子の動きや温度の効果は取り入れることはできない。しかしながら、多くの場合、対象となる材料を構成する分子そのものの個性が材料全体の主たる性質を特徴づけており、材料設計の方向性や問題の特定などへ大いに役立てることができる。ただし、温度や溶媒などの環境の効果が無視できない場合は、分子動力学計算と組み合わせるなど、何らかの工夫が必要になってくる。
2. 計算手法と基底関数
残念ながら、一般の分子のSchrödinger方程式を厳密に解くことは非常に困難であり、量子化学ではいくつかの近似が導入される。論文などでは、量子化学の計算条件を「B3LYP/6-31+G(d,p)」のような形式で記述するが、ここでB3LYPとは計算手法の種類を意味しており、Schrödinger方程式の近似方法の種類を表している。しかしその近似だけではSchrödinger方程式を解くことは難しいので、波動関数を既知の関数の線形結合で表すという近似がさらに導入される。6-31+G(d,p)とはその関数の種類を表しており、基底関数と呼ばれる。実際の量子化学計算では、この計算手法と基底関数に何を採用するかによって計算精度や計算時間が決定づけられる。
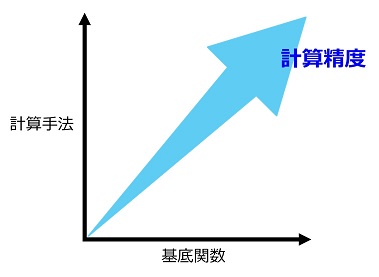
注意すべきことは、計算手法と基底関数はまったく独立の概念であり、混同してはならないということである。特に、DFTに関連する計算手法の種類は「汎関数」と呼ばれることもあるため、基底関数と混同しやすく、注意が必要である。
3. 量子化学計算でわかること
ひとたび波動関数がわかれば、分子に関するさまざまな情報が得られる。
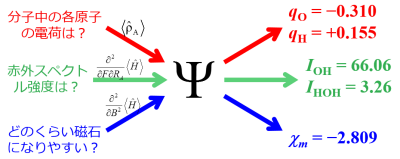
例えば、HOMO/LUMOなどの分子軌道(MO)は分子の安定性や反応性について議論するために利用される。特に、酸化還元電位とHOMO/LUMOエネルギーは密接な関係にあることが多く、基本的にHOMOが高いほど酸化しやすく、LUMOが低いほど還元されやすい。
また、分子構造や置換基の情報を与える赤外・ラマンスペクトルやNMRスペクトル、光による電子励起に関連したUV-VisスペクトルやCDスペクトルの計算結果は、さまざまな分光測定の結果と直接比較が可能であり、ピークの帰属や解析に利用される。そのほか、分子の最適化構造や原子電荷(atomic charge)、双極子・多極子モーメントなども計算により得られる。
4. 基底状態計算手法の種類
計算手法の精度(信頼性)はコスト(計算時間)とトレードオフの関係にあり、欲しい精度と許容できる計算時間との兼ね合いから実際の計算条件が決定される。
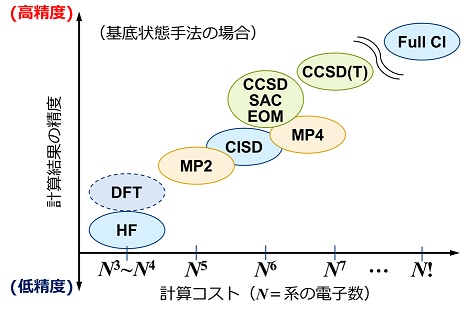
通常の分子の計算では密度汎関数法(DFT)がよく利用されている。この方法は、Schrödinger方程式の代わりに、それと等価なKohn-Sham方程式に基づいている。Schrödinger方程式ではN個の電子の座標をまともに取り扱うのに対し、Kohn-Sham方程式ではたった1個の電子の座標を取り扱う形となっている。そのため、DFT法は圧倒的に計算が高速である。ただし、DFTでは外部パラメータとして交換相関汎関数(または単に「汎関数」)が必要であり、汎関数の質がDFT計算結果に大きな影響を与える。現在最もよく用いられている汎関数はB3LYPであり、欠点もあるものの、計算時間の割にそこそこ良い結果を与えることが多い。
DFTで満足いく結果が得られない場合は、計算時間と引き換えに、さらに高精度の計算手法が必要となる。その場合によく用いられる手法は、二次のMøller-Plesset摂動法(MP2)であり、それでも満足できない場合には四次の摂動法(MP4)や一電子および二電子クラスター展開法(CCSD)などが利用される。
5. 励起状態計算手法の種類
励起状態の場合も、基底状態と同様、計算手法の精度とコストはトレードオフの関係にある。
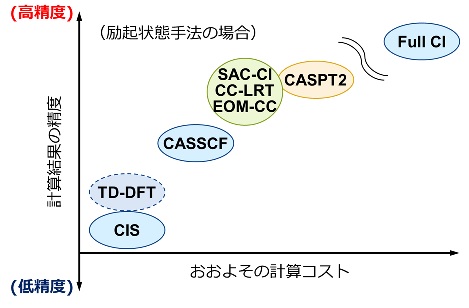
励起状態の計算では時間依存密度汎関数法(TD-DFT)が最もよく用いられている。TD-DFTはDFT同様、コストパフォーマンスが高く、特に価電子励起は短時間で比較的良く実験傾向を再現する。一方、長距離の電子移動(CT)を伴うような励起については正しい結果を与えないことが多い。このような問題に対しては長距離相互作用を考慮した汎関数(例えば、ωB97XDやCAM-B3LYPなど)を用いることで対応可能である。
長距離補正汎関数でも対応できないような問題に対しては、より精度の保証されたSAC-CI法などが利用される。
お問い合わせ
平日9:30~17:30 (土曜日、日曜日、祝祭日、年末年始、夏期休暇は、休日とさせていただきます。)

