Science as a Service
Learning Contents
量子化学計算学習コンテンツ
第2章 本格的な計算を行う前に…
サンプルページ
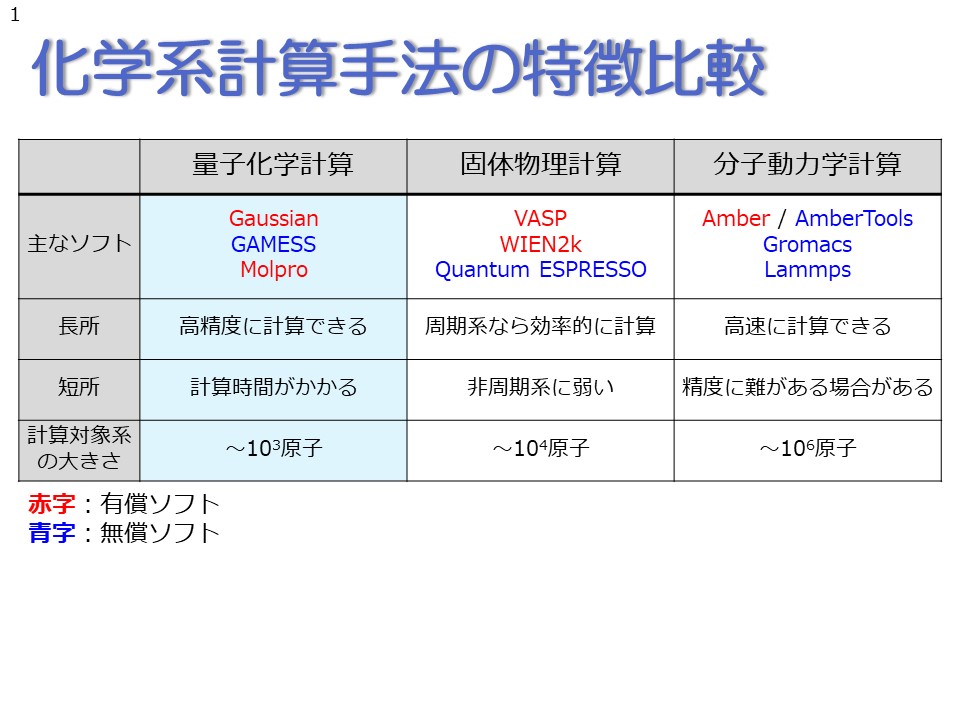 |
化学で良く用いられる量子化学計算・固体物理計算・分子動力学計算の3つの特徴について、もう少し詳しく見ていきましょう。 量子化学計算では、後ほど説明するシュレーディンガー方程式を、なるべく近似を加えずに精密に解いています。シュレーディンガー方程式とは、ミクロの世界の法則を支配する基本方程式であり、これをなるべく近似せずに解くことで、対象系を高精度に計算できます。しかしその反面、他のシミュレーション方法に比べて計算時間がかかることが欠点であり、一般的な性能のワークステーションと呼ばれるコンピュータを用いて、現実的な時間で量子化学計算ができるのは、おおよそ1000原子程度までとなります。さらに言えば、原子数が多くなると、ユーザーが工夫をしない限り、方程式の解が収束しづらくなるため、計算初心者が量子化学計算を行う場合は、200原子程度までと思っておいた方が無難でしょう。 このような計算対象の原子数の制限があるため、量子化学計算で取り扱えるのは、主に1分子の性質で代表できるような物性や現象、例えば有機化学反応や分子の吸収・発光現象等となります。 一方、分子動力学計算は、量子化学計算とは対照的に、おおよそ数十万原子を超える大規模な系を高速に計算できるという特徴を持ちます。したがって、分子動力学計算は、例えば密度や粘度等のような、1分子の特性ではなく多数の分子の存在により特徴づけられる現象を記述することができます。 分子動力学では、分子の特性を特徴づける電子の効果を「力場」と呼ばれるパラメータに押し込めることによって、計算の簡略化と高速化を実現しています。分子動力学計算の信頼性はこの力場の信頼性に大きく依存し、活発に研究されている水分子やペプチド・タンパク質等では比較的良い結果を得ることができますが、あまり研究されていない分子系では精度に難がある場合がありますので、注意が必要です。 固体物理計算は、量子化学計算と分子動力学計算の間の立ち位置ですが、どちらかというと量子化学計算に近い性格を持っています。固体物理計算は、量子化学計算からさらに少し近似を加えることにより、高速かつ高精度に計算することができるという特徴を持っています。その代わり、固体物理計算の対象系は、単位格子の構造が無限に繰り返し現れる周期系に限定され、孤立分子系や非周期的な系は本質的には計算できません。 なお、第一原理計算と呼ばれるシミュレーション方法がしばしば教科書や論文等に登場しますが、これは多くの場合、固体物理計算のことを指します。 |
|---|---|
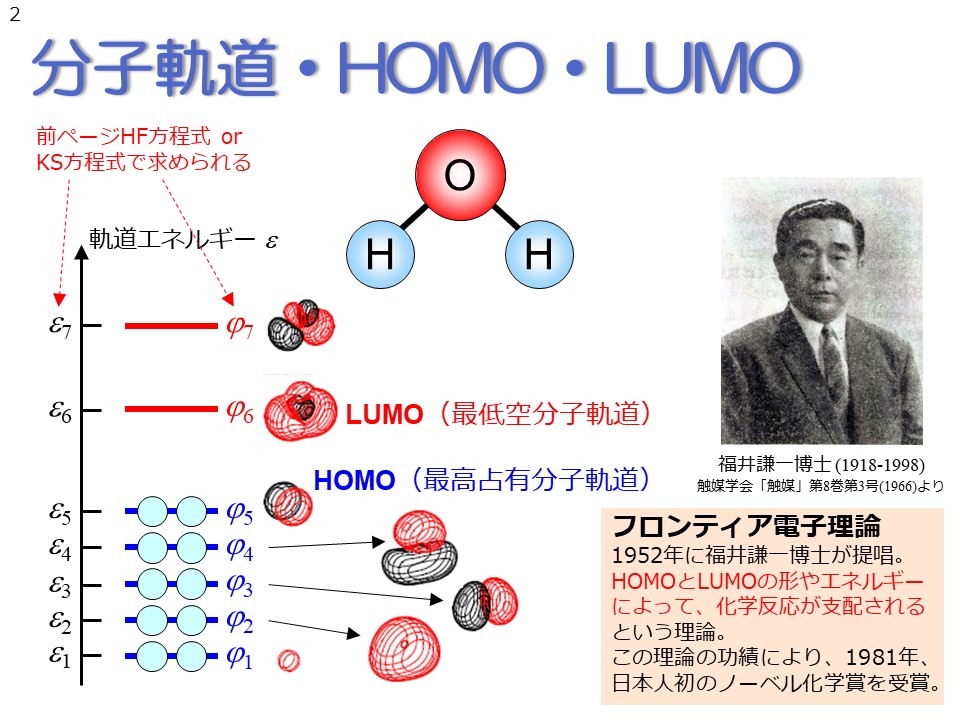 |
ハートリー-フォック法またはDFT法では、分子中の電子は、分子軌道と呼ばれる軌道に収容されます。各分子軌道は分子構造により決定される固有の形状と軌道エネルギーを持っています。この各軌道の形状を表す関数φとエネルギーεを決める方程式が、前ページのハートリー-フォック方程式またはコーン-シャム方程式になります。 通常、分子中の電子は、軌道エネルギーの低い方から順に2個ずつ電子が分子軌道に収容されていきます。例えば水分子の場合、電子は全部で10個ありますので、下から5番目の分子軌道まで電子が2個ずつ収容され、それより高い軌道には電子は入っていないという状態になります。 これらの分子軌道のうち、最も重要とされる分子軌道が、HOMO・LUMOと呼ばれる軌道です。HOMOは最高占有分子軌道と訳され、電子が入っている軌道の中で最も高いエネルギーを持つ軌道のことを指します。LUMOは最低空分子軌道と訳され、電子が入っていない空の軌道の中で最もエネルギーが低い軌道のことです。 このHOMOとLUMOの形やエネルギーこそが化学反応を支配するのだという理論を、フロンティア電子理論と言い、この理論を提唱したのが、福井謙一先生です。福井先生は、この理論の功績により、1981年、日本人初のノーベル化学賞を受賞致しました。 |
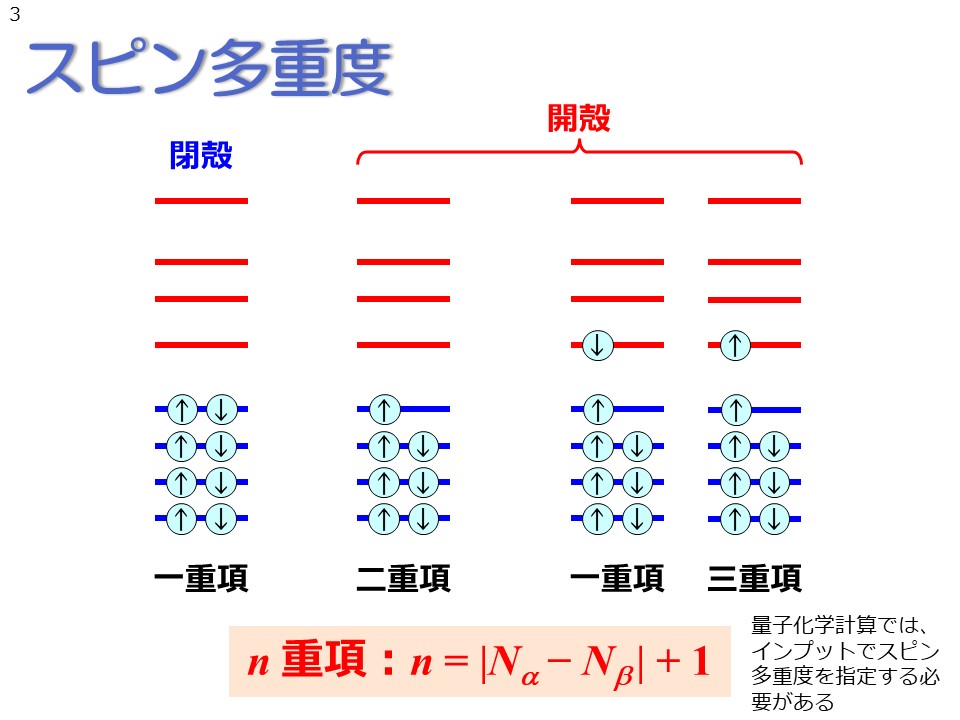 |
その系でのαスピン電子の数とβスピン電子の数から、スピン多重度と呼ばれる値を求めることができます。スピン多重度nはこのように、αスピン電子数とβスピン電子数の差に1を足して求められます。また、スピン多重度がnである状態のことを、n重項と呼びます。例えば、先程説明した閉殻状態では、αスピンの数とβスピンの数が等しいため、n=1、すなわち一重項となります。 閉殻に対する用語は、「開殻」です。開殻とは、電子が1個だけ収容された軌道を含んだ状態のことを指します。例えば、αスピン電子がβスピン電子より1個多いラジカル分子は、電子1個の軌道を1つ含んでいるため、開殻系となります。この場合のスピン多重度は2であり、二重項と呼ばれます。 電子1個の分子軌道が2つある系では、それらの孤立した電子が異なるスピンを持つか同じスピンを持つかで、スピン多重度が異なります。スピン多重度の式を実際に計算してみるとわかりますが、異なるスピンを持つ場合は一重項、同じスピンを持つ場合は三重項となります。 Gaussianをはじめとする量子化学計算では、このスピン多重度をユーザが指定してやる必要があります。ほとんどの分子は閉殻状態ですので、スピン多重度は通常1であると覚えておくとよいでしょう。 |
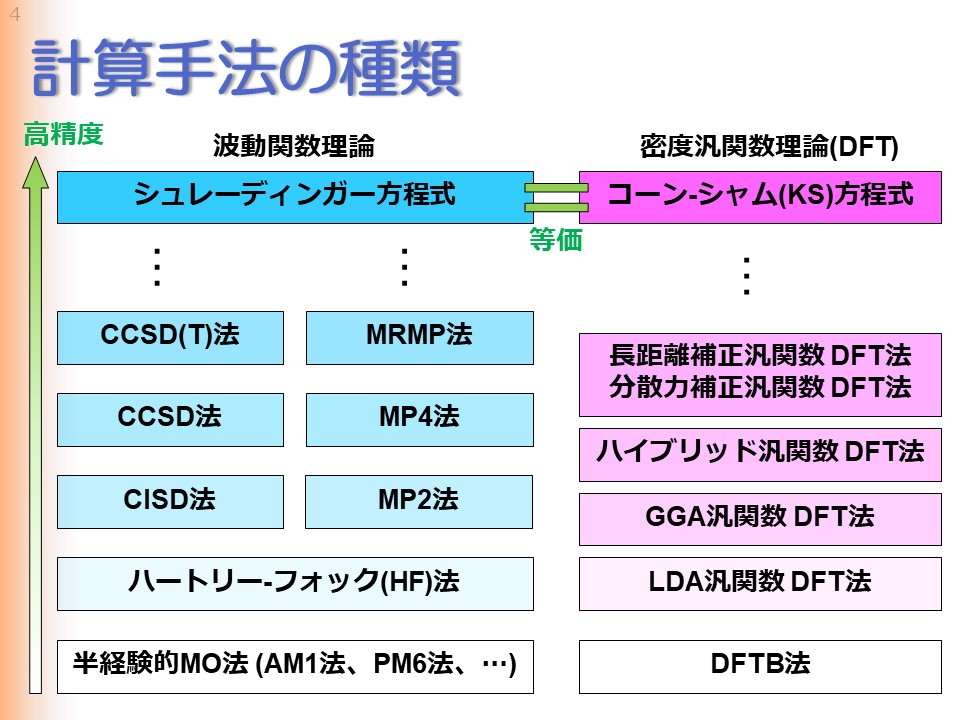 |
それではまず計算手法の種類について紹介致します。 何度も申し上げている通り、本来はシュレーディンガー方程式を解きたいのですが、この方程式を解くことは事実上不可能なので、近似的にシュレーディンガー方程式を解くことが行われます。シュレーディンガー方程式の近似的解法として最も基本的なものはハートリー-フォック法と呼ばれるもので、ほとんどの理論はこの方法がベースとなっています。また大規模な分子ではハートリー-フォック法でも時間がかかるため、半経験的MO法と呼ばれる、低精度ながら高速な計算手法がしばしば用いられます。一方、ハートリー-フォックの精度を改善し、シュレーディンガー方程式の精度に近づける方法としては、二通りの手段があり、それぞれにさまざまな計算手法が提案されています。これらの手法の詳細はここでは示しません。ひとまずは、このようにさまざまな計算手法があるのだということだけ頭に入っていれば十分です。 さて、これらの手法は、近似的にでも波動関数を求めるための手法であり、まとめて波動関数理論と呼ばれます。一方、シュレーディンガー方程式とは別の理論である、密度汎関数理論、通称DFTに基づいたコーン-シャム方程式というものも提案されています。このコーン-シャム方程式は、実はシュレーディンガー方程式と等価であることがわかっています。すなわち、コーン-シャム方程式を厳密な形で解くことができれば、シュレーディンガー方程式を解いたのと同じ答えが得られることになるのです。ただ残念ながら、このコーン-シャム方程式の厳密な形は不明であるため、前節でも述べた通り、現実のコーン-シャム方程式は近似方程式となります。 DFTの近似方法としては、精度の低い順に、LDA汎関数DFT・GGA汎関数DFT・ハイブリッド汎関数DFTというように、こちらもさまざまな種類があります。また、LDA-DFT法よりさらに高速な方法としてDFTB法があり、こちらは大規模な分子の計算で利用されることがあります。 |
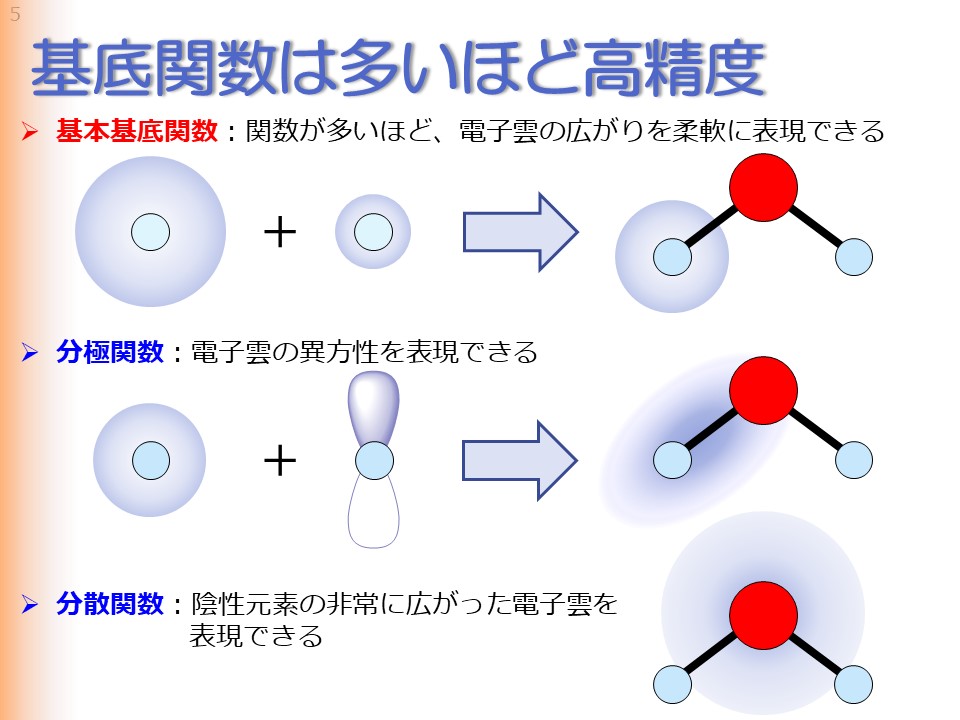 |
基底関数は、その数が多くなるほど高精度の計算結果を与えます。水分子の場合を例にとりましょう。 原子の水素は1s軌道が正確な波動関数となります。しかし分子中の水素が持つ電子雲は、周りの原子の影響を受けて、水素原子の電子雲とは異なっているはずです。さらに言えば、水分子中の水素原子、アンモニア中の水素原子、メタン中の水素原子もまた、それぞれ微妙に異なった電子雲を持つはずです。しかし水素に1sの基底関数だけを与えると、どんな分子でも水素原子と同じ電子雲となってしまい、分子中の水素を精度良く表現することができません。そこで、広がったs軌道とコンパクトなs軌道の2個の基底関数を水素に与えてやると、それらの線形結合を取ることにより、分子中の水素の電子雲の広がりを柔軟に表現することができ、計算精度を上げることができます。 分極関数は電子雲の異方性を表現するために加えられる基底関数です。水分子中の水素原子の電子雲は、酸素原子との結合方向に異方性を持っていますが、この異方性は水素原子の基本基底関数だけでは表現できません。なぜなら、s軌道にどれだけs軌道を重ねてもs軌道にしかならないからです。電子雲の異方性を表現するためには、より角運動量の高い軌道が必要であり、このような役割を持った基底関数を分極関数といいます。この場合、水素原子にp軌道の分極関数を加えることで初めて、酸素原子との結合方向の異方性を表現することが可能になります。 また、分散関数は主に陰性元素の非常に広がった電子雲を表現するために用いられる基底関数です。陰性の原子はアニオンになると電子雲が非常に広がることが知られていますが、分子中の陰性原子も隣接する原子から電子を吸引し、アニオンに近い状態になっていると考えられます。このようなアニオンに近い状態の電子雲を表現するための基底関数が分散関数です。分散関数は、特にハロゲンを含む分子で重要な役割を果たします。 |
お問い合わせ
Contact
お問い合わせ
お客様に最適な製品をご提案いたします。まずは気軽にお問い合わせ下さい。
075-353-0120
平日9:30~17:30 (土曜日、日曜日、祝祭日、年末年始、夏期休暇は、休日とさせていただきます。)

