Technical Information

技術情報

ホーム > HPC・DL・AI > 技術情報 > ベンチマーク情報 > N体問題プログラムのインテル® Xeon Phi™ コプロセッサー向け移植の評価

N体問題プログラムのインテル® Xeon Phi™ コプロセッサー向け移植の評価

HPCに最適な処理を実現するためにインテルから満を持して登場したインテル Xeon Phi コプロセッサー。競合製品に対するプログラミングの容易さと、その競合製品に匹敵する性能との両立をアピールしているこの製品ですが、実際のプログラミング作業がどこまで容易であるか、またその結果としての性能はどのようなものであるか、検証を行いました。
結果、Phi向けにコンパイルしなおすだけでE5-2680 x2CPUの約2倍、組み込み命令を使ったチューニングをすると約7～9倍の実効性能が得られました。

ベンチマーク環境

製品名	HPC5000-XSPHI4R2S
プロセッサー	インテル Xeon E5-2680（8コア、2.70GHz）×2CPU
コプロセッサー	インテル Xeon Phi 5110P ×2
メモリー	16GB Registered ECC DDR3 1600MHz ×8（計128GB）
OS	CentOS 6.3 x86_64
コンパイラー	インテル C++ Composer XE 2013 Update 2（icpc 13.1.0.146）
MPI	インテル MPI ライブラリー 4.1
コンパイルオプション (Xeon E5)	-ipo -O3 -xHost -no-prec-div
コンパイルオプション (Xeon Phi)	-ipo -O3 -mmic -no-prec-div

プログラム

チューニング前のN体問題プログラムは、以下のようなものです（主要部分の抜粋）。

template<typename T>
struct vec3_t {
  T *x;
  T *y;
  T *z;
};

template<typename T> static void
update(int n, vec3_t<T> *newX, vec3_t<T> *oldX, T *m, vec3_t<T> v)
{
  const T dt = (T) 0.016;
  const T eps = (T) 0.1;
#pragma omp parallel for
#pragma vector aligned
#pragma ivdep
  for (int i = 0; i < n; ++i) {
    T xi = oldX->x[i];
    T yi = oldX->y[i];
    T zi = oldX->z[i];
    T ax = (T) 0.0;
    T ay = (T) 0.0;
    T az = (T) 0.0;
    for (int j = 0; j < n; ++j) {
      T xj = oldX->x[j];
      T yj = oldX->y[j];
      T zj = oldX->z[j];
      T rx = xj - xi;
      T ry = yj - yi;
      T rz = zj - zi;
      T r2 = rx * rx + ry * ry + rz * rz + eps;
      T r_r = (T) 1.0 / std::sqrt(r2);
      T r_r3 = r_r * r_r * r_r;
      T s = m[j] * r_r3;
      ax += rx * s;
      ay += ry * s;
      az += rz * s;
    }
    T vxi = v.x[i] + ax * dt;
    T vyi = v.y[i] + ay * dt;
    T vzi = v.z[i] + az * dt;
    xi += vxi * dt;
    yi += vyi * dt;
    zi += vzi * dt;
    newX->x[i] = xi;
    newX->y[i] = yi;
    newX->z[i] = zi;
    v.x[i] = vxi;
    v.y[i] = vyi;
    v.z[i] = vzi;
  }
  vec3_t<T> tmpX = *oldX;
  *oldX = *newX;
  *newX = tmpX;
}

このプログラムをそのままコンパイルして実行すると、以下の性能となります。

表1　未チューニング時のベンチマーク結果（N=65,536）

	Xeon E5-2680 x2	Xeon Phi 5110P x1	高速化率
単精度	164.836 GFlops	313.188 GFlops	1.900倍
倍精度	55.430 GFlops	135.721 GFlops	2.449倍

特定のアーキテクチャーに対してチューニングしていないプログラムですが、単にコンパイルし直してPhi 5110P上でnative実行するだけで、E5-2680 x2構成に対して約2倍の性能向上を実現しています。

インテルXeon Phiコプロセッサーへの最適化

上記のプログラムをコンパイルする際、インテル C++ Composer XEの自動ベクトル化機能により、内側のループjがベクトル化されます。このとき、ループ一周あたり19 Flopの計算に対して倍精度の場合32 Byteのメモリアクセスが発生し、Xeon Phi 5110Pの1,011 GFlops 対 320 GB/sの仕様を考えると、メモリアクセスがボトルネックとなっていることが分かります。このボトルネックを軽減するために、ベクトル化するループを、内側ではなく外側のiに変更する手法がよく知られています。そこで、外側のループで登場する変数を、インテルMICアーキテクチャーのSIMD命令に一対一対応する組み込み命令を使ってベクトル化し、この手法を実装しました。このチューニング後の単精度版・倍精度版のプログラムをそれぞれ次に示します。

#include <micvec.h>

template<> static void
update<float>
(int n, vec3_t<float> *newX, vec3_t<float> *oldX, float *m, vec3_t<float> v)
{
  const __m512 dt = _mm512_set1_ps((float) 0.016);
  const __m512 eps = _mm512_set1_ps((float) 0.1);
#pragma omp parallel for
  for (int i = 0; i < n; i += 16) {
    __m512 xi = _mm512_load_ps(oldX->x + i);
    __m512 yi = _mm512_load_ps(oldX->y + i);
    __m512 zi = _mm512_load_ps(oldX->z + i);
    __m512 ax = _mm512_setzero_ps();
    __m512 ay = _mm512_setzero_ps();
    __m512 az = _mm512_setzero_ps();
    for (int j = 0; j < n; ++j) {
      __m512 xj = _mm512_set1_ps(oldX->x[j]);
      __m512 yj = _mm512_set1_ps(oldX->y[j]);
      __m512 zj = _mm512_set1_ps(oldX->z[j]);
      __m512 rx = _mm512_sub_ps(xj, xi);
      __m512 ry = _mm512_sub_ps(yj, yi);
      __m512 rz = _mm512_sub_ps(zj, zi);
      __m512 r2 =
        _mm512_fmadd_ps(rz, rz,
                        _mm512_fmadd_ps(ry, ry,
_mm512_fmadd_ps(rx, rx, eps)));
      __m512 r_r = _mm512_rsqrt23_ps(r2);
      __m512 r_r3 =
        _mm512_mul_ps(r_r, _mm512_mul_ps(r_r, r_r));
      __m512 s = _mm512_mul_ps(_mm512_set1_ps(m[j]), r_r3);
      ax = _mm512_fmadd_ps(rx, s, ax);
      ay = _mm512_fmadd_ps(ry, s, ay);
      az = _mm512_fmadd_ps(rz, s, az);
    }
    __m512 vxi = _mm512_load_ps(v.x + i);
    __m512 vyi = _mm512_load_ps(v.y + i);
    __m512 vzi = _mm512_load_ps(v.z + i);
    vxi = _mm512_fmadd_ps(ax, dt, vxi);
    vyi = _mm512_fmadd_ps(ay, dt, vyi);
    vzi = _mm512_fmadd_ps(az, dt, vzi);
    xi = _mm512_fmadd_ps(vxi, dt, xi);
    yi = _mm512_fmadd_ps(vyi, dt, yi);
    zi = _mm512_fmadd_ps(vzi, dt, zi);
    _mm512_store_ps(newX->x + i, xi);
    _mm512_store_ps(newX->y + i, yi);
    _mm512_store_ps(newX->z + i, zi);
    _mm512_store_ps(v.x + i, vxi);
    _mm512_store_ps(v.y + i, vyi);
    _mm512_store_ps(v.z + i, vzi);
  }
  vec3_t<float> tmpX = *oldX;
  *oldX = *newX;
  *newX = tmpX;
}

図1　インテルMIC向け組み込み命令を使ったソースコード例（単精度）

#include <micvec.h>

template<> static void
update<double>
(int n, vec3_t<double> *newX, vec3_t<double> *oldX, double *m, vec3_t<double> v)
{
const __m512d dt = _mm512_set1_pd((double) 0.016);
const __m512d eps = _mm512_set1_pd((double) 0.1);
const __m512d c05 = _mm512_set1_pd((double) 0.5);
const __m512d c15 = _mm512_set1_pd((double) 1.5);
#pragma omp parallel for
for (int i = 0; i < n; i += 8) {
__m512d xi = _mm512_load_pd(oldX->x + i);
__m512d yi = _mm512_load_pd(oldX->y + i);
__m512d zi = _mm512_load_pd(oldX->z + i);
__m512d ax = _mm512_setzero_pd();
__m512d ay = _mm512_setzero_pd();
__m512d az = _mm512_setzero_pd();
for (int j = 0; j < n; ++j) {
__m512d xj = _mm512_set1_pd(oldX->x[j]);
__m512d yj = _mm512_set1_pd(oldX->y[j]);
__m512d zj = _mm512_set1_pd(oldX->z[j]);
__m512d rx = _mm512_sub_pd(xj, xi);
__m512d ry = _mm512_sub_pd(yj, yi);
__m512d rz = _mm512_sub_pd(zj, zi);
__m512d r2 =
_mm512_fmadd_pd(rz, rz,
_mm512_fmadd_pd(ry, ry,
_mm512_fmadd_pd(rx, rx, eps)));
__m512 r2_ps = _mm512_cvtpd_pslo(r2);
__m512d r2_05 = _mm512_mul_pd(r2, c05);
__m512 r_r_ps = _mm512_rsqrt23_ps(r2_ps);
__m512d r_r = _mm512_cvtpslo_pd(r_r_ps);
r_r =
_mm512_mul_pd(r_r,
_mm512_fnmadd_pd(_mm512_mul_pd(r2_05, r_r),
r_r, c15));
r_r =
_mm512_mul_pd(r_r,
_mm512_fnmadd_pd(_mm512_mul_pd(r2_05, r_r),
r_r, c15));
__m512d r_r3 =
_mm512_mul_pd(r_r, _mm512_mul_pd(r_r, r_r));
__m512d s = _mm512_mul_pd(_mm512_set1_pd(m[j]), r_r3);
ax = _mm512_fmadd_pd(rx, s, ax);
ay = _mm512_fmadd_pd(ry, s, ay);
az = _mm512_fmadd_pd(rz, s, az);
}
__m512d vxi = _mm512_load_pd(v.x + i);
__m512d vyi = _mm512_load_pd(v.y + i);
__m512d vzi = _mm512_load_pd(v.z + i);
vxi = _mm512_fmadd_pd(ax, dt, vxi);
vyi = _mm512_fmadd_pd(ay, dt, vyi);
vzi = _mm512_fmadd_pd(az, dt, vzi);
xi = _mm512_fmadd_pd(vxi, dt, xi);
yi = _mm512_fmadd_pd(vyi, dt, yi);
zi = _mm512_fmadd_pd(vzi, dt, zi);
_mm512_store_pd(newX->x + i, xi);
_mm512_store_pd(newX->y + i, yi);
_mm512_store_pd(newX->z + i, zi);
_mm512_store_pd(v.x + i, vxi);
_mm512_store_pd(v.y + i, vyi);
_mm512_store_pd(v.z + i, vzi);
}
vec3_t<double> tmpX = *oldX;
*oldX = *newX;
*newX = tmpX;
}

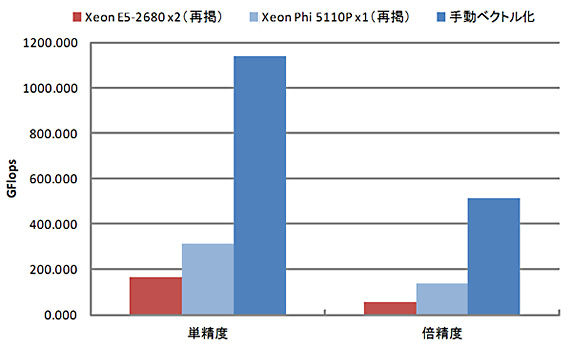
図2　インテルMIC向け組み込み命令を使ったソースコード例（倍精度）

表2　インテルMIC向け組み込み命令によるチューニング時のベンチマーク結果

	Xeon E5-2680 x2 （再掲）	Xeon Phi 5110P x1 （再掲）	手動ベクトル化	対E5	対Phi
単精度	164.836 GFlops	313.188 GFlops	1138.728 GFlops	6.908倍	3.636倍
倍精度	55.430 GFlops	135.721 GFlops	510.918 GFlops	9.217倍	3.764倍

プログラムの移植性は悪くなりましたが、性能をさらに3倍上乗せし、単精度で1 TFlopsの大台に乗せることができました。なお、CUDA版のN体問題プログラム（N=65536）ではNVIDIA Tesla K20M x1で単精度1,268 GFlops、倍精度555 GFlopsが出ますので、それにほぼ匹敵する性能が得られています。

結論

単純にプログラムを再コンパイルするだけで性能向上を得られるだけでなく、相応のチューニングを行えばTesla K20に肉薄する性能を得られるという点で、一粒で二度おいしい製品と言えるでしょう。特に自らの手でアルゴリズムを開発されることの多いお客様の場合、まず汎用的な実装をscrap and buildしながらアルゴリズムの効用を確認された後、性能向上のためのチューニングに着手されることも多いと思われますが、そのような開発プロセスを単独製品で両立させるインテル Xeon Phi コプロセッサーを、第一の選択肢として推奨いたします。