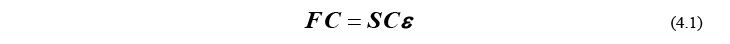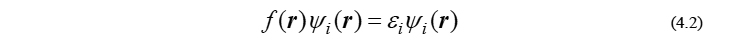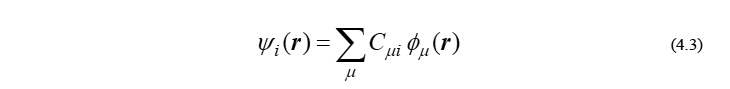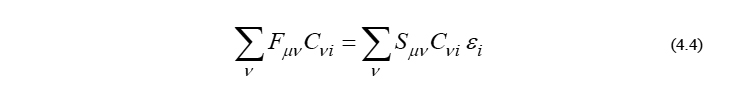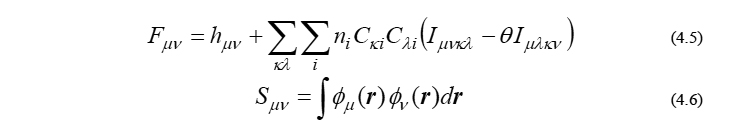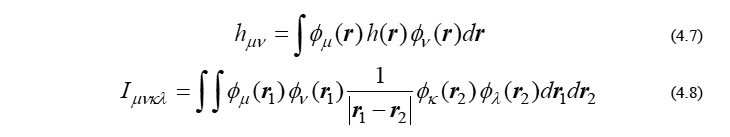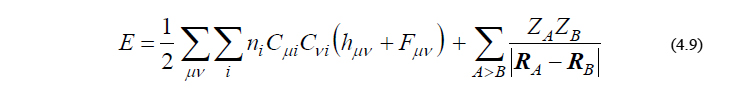計算化学 ソフトウェア

「計算がエラーで止まってしまった！でもどうすればいいかわからない。」
「結果が何かおかしい。どこがいけなかったのだろうか？」
といった疑問の解決に少しでもお力添えするべく、よくあるエラーを中心に、直接的な対処法から簡単な理論的背景まで含めて解説いたします。

第４回配信：　量子化学計算の流れ

　前回までの配信では「第１部　基礎編：GaussianエラーのFirst Aid」と題し、初心者が起こしがちなエラーや、簡単に対処可能なエラーについてお話ししてきました。しかし、Gaussianにはもっと多くの複雑なエラー状況が存在し、それらのエラーに本格的に対処していくには、そのエラーが起こる理屈から理解する必要があります。そこで今回から「第２部　Gaussianでエラーが起こる仕組みを知る」と題し、Gaussian計算の流れとその流れの中で起こり得るエラーについて解説していきます。今回の配信では、まず量子化学計算の一般的な流れについて見ていきましょう。

(4-1）　計算の流れを知ることの重要性：　エラー対処の視点から

　物を作るには大抵手順というものがあります。ケーキやハンバーグを作る時にも手順がありますし、Gaussianが計算を行う時にも手順があります。この手順のどこかで何か正しくないことがあると、ケーキやハンバーグの場合は失敗作、Gaussian計算の場合ではエラー（結果がおかしい）、ということになるわけですが、その手順を知らなければ、たとえ「どう失敗した」「どう結果がおかしい」ということがわかっても結局それ以上先のステージに進むことができません。
　例えば、ハンバーグを作る場合の手順は、大雑把に

(1)　必要な食材（挽き肉、玉ねぎ、パン粉、卵、調味料）を必要な分だけ用意する
(2)　玉ねぎをみじん切りにして、炒める
(3)　パン粉に水を加えて、よく絞る
(4)　挽き肉に卵、塩、コショウ、(2)(3)で出来たものを加え、練り合わせる
(5)　(4)で出来た物をハンバーグ形に整え、両手でキャッチボールして空気を抜く
(6)　(5)で出来た物の真ん中を凹ませてから、焼く
(7)　(6)で出来た物を引っくり返し、反対側を焼く
(8)　(7)で出来た物を皿に盛り付け、ソースをかけて完成

となりますが、例えば「ハンバーグを焼いたら上面が破裂してしまった」「肉汁が外に出てきてパサパサになってしまった」時に、上記の手順の意義や注意点が理解できていなければ、なぜ失敗したのかがわかりません。答えから先に言うと、破裂してしまったのは(6)でのハンバーグの凹ませが足りなかったから、パサパサになってしまったのは(4)での練り合わせが足りなかったからで、材料や焼き方を改善してもこの場合は根本的な解決にはなりません。Gaussianのエラーも同じことで、正しくない基底関数で計算しても正しい結果が得られませんが、その時に「分子構造やエネルギー収束条件の不良でなく、基底関数の不良が原因だ」と特定できるようになるためには、Gaussianでの計算手順を正しく理解する必要があります。
　Gaussianでの計算手順は、アウトプットファイル（以下、アウトプット）と密接な関係にあります。なぜなら、アウトプットは計算の流れ（ハンバーグの例で言えば、(1)～(8)の手順）に沿って打ち出され、かつ、各手順で必要なチェック（例えるなら、十分に材料を練り合わせたか、ちゃんと肉を凹ませたか等）の結果が全て記録されているからです。したがって、アウトプットを読みこなすことができれば、計算のどこでどんなエラーが起こって、どう解決すればよいのかがわかるようになります。そのためにも、下準備としてまず、量子化学計算の大まかな流れを理解しておきましょう。

（4-2）　一点計算の計算手順（HFおよびDFTの場合）

　まず、実際によく利用されるDFT一点計算（エネルギー計算）の場合を解説します。Hartree-Fock （以下、HF）法も、DFTとは計算式が一部異なるだけで計算手順はほとんど同じなので、一緒に解説します。
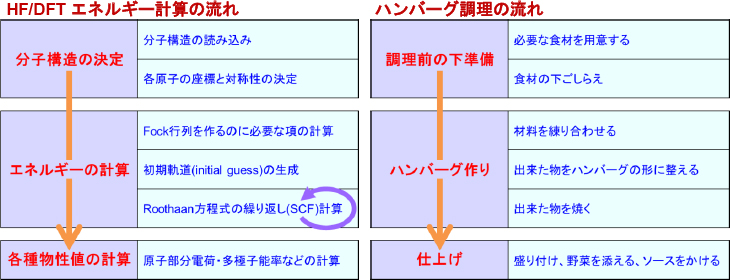
　HF/DFT一点計算の流れを下の図に示します。また、この流れをハンバーグの調理で例えたものがその右の図です。このように計算や調理の流れを幾つかのプロセスの連なりとして表すことは、失敗対策という観点では、どこに失敗の原因があったかが明確になるという点で非常に重要です。Gaussianでは、これらの各プロセス内で作業すべき内容が明確に定義されており、計算が不首尾に終わった場合、少なくともどのプロセスで異常が起こったのかがわかりやすくなるように設計されています。

　上の図より、計算全体の流れを大雑把にまとめると、「分子構造の決定」「エネルギー（と波動関数）の計算」「（求まった波動関数から）各種物性値の計算」という３つのパートからなることがわかります。このうち、「分子構造の決定」の作業内容はほぼ自明ですし、「物性値の計算」でエラーが起こることは通常ありませんので、残りの「エネルギーの計算」パートの中身をもう少し詳しく見てみましょう。
　HF/DFTエネルギーを求めるには、以下のRoothaan方程式と呼ばれる方程式を解く必要があります。

ここで、F はFock行列、S は重なり行列、C は軌道係数行列、ε は軌道エネルギー行列と呼ばれます。式(4.1)において重要なポイントは、行列 F と S がこの方程式のインプットパラメータで、方程式の解として C と ε が求められるということです（この C と ε が求まれば、直ちにエネルギーが計算できます）。
　さて、このRoothaan方程式を解くには前準備が必要です。まず F と S を作るには基底関数の情報とそれに付随する積分計算が必要であり、これを上図の「Fock行列を作るのに必要な項の計算」プロセスで行います。次に、S を作るにはそれだけで十分なのですが、F を作るにはそれだけでは足りません。というのも、F は（本来答えとなる）C に依存する行列であり、C が与えられないと F を決めることができないのです。そこでまず、C の初期値 C₀ を適当に与えてF を計算します。この初期値 C₀ のことを初期軌道（initial guess）と呼び、C₀ を与える作業を上図の「初期軌道（initial guess）の生成」プロセスで行います。その後にRoothaan方程式を解くと C と ε が求まるのですが、このままでは、求まった C と、F の中に含まれている C は一いたしていません。そこで、新たに求まった C を用いて Fを更新し、再び方程式を解いて、そこから得られる C を用いて F を更新し……という手続きを C がもはや変わらなくなるまで繰り返して、最終的な解を得ます。この手続きは自己無矛盾な場、または自己無撞着な場（Self-consistent field; SCF）の方法と呼ばれ、この作業を上図における「Roothaan方程式の繰り返し（SCF）計算」プロセスで行います。
　余談ですが、このSCF手続きの中で、ある C₀ から始めてそのような無矛盾な C が見つかるかどうかは、実は自明な問題ではありません。ですから、妥当な分子構造、基底関数を与えているにも拘らず、エネルギーが収束しない場合は、このSCF手続きが上手く働かなかったか、C₀ が悪かったかのどちらかの可能性が高いです。（詳しくは、第１１回、第１２回配信で解説します。）

（4-3）　分子構造最適化の計算手順（HFおよびDFTの場合）

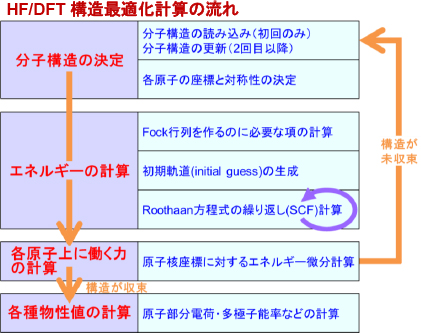
　次に構造最適化計算の場合を解説いたします。Gaussianでの分子構造最適化は、あらかじめ与えられた初期分子構造で各原子に働く力を計算し、その力のベクトル方向に各原子を動かし、動かした後の構造で各原子に働く力を計算し、またその力のベクトル方向に各原子を動かし……という手続きを、全ての原子上の力が無くなるまで繰り返すことにより行われます。この「原子に働く力」は、その時点の分子構造におけるRoothaan方程式を解いてHF/DFTエネルギーを計算し、そのエネルギーを原子の座標（正確に言うと、原子核座標）で微分することにより得られます。
　以上をまとめると、下図のようになります。

一点計算と違うのは、「原子核座標に対するエネルギー微分計算」プロセスを新たに行う必要があることと、力が収束するまで「分子構造の更新」～「原子核座標に対するエネルギー微分計算」の手続き（これが構造最適化の１ステップに相当します）を繰り返す必要があることです。HF/DFT計算の場合、この１ステップ内で力の計算がエネルギー計算と同程度の時間を要するため、構造最適化全体にかかる時間は、N を構造最適化ステップ数として、一点計算のおおよそ2N 倍となります。（分子構造の決定・各種物性値の計算は、通常ほとんど時間がかかりません。）
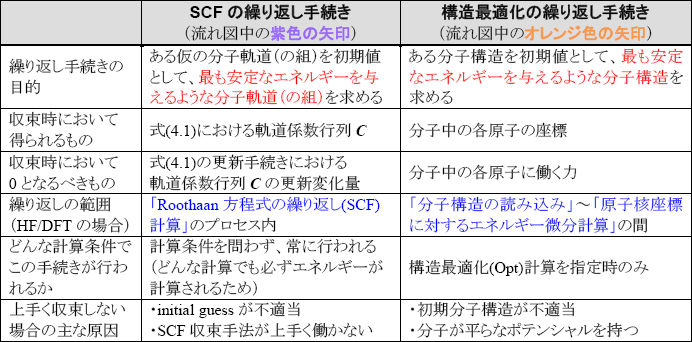
　ここで、注意すべき点として、この構造最適化ステップの繰り返し手続きと、(4-2)節で説明したSCF計算の繰り返し手続きを混同してはならないことを強調しておきます。しかも紛らわしいことに、どちらの繰り返し手続きでも「Opt」「Optimization」という言葉がしばしば使用されるため、Gaussian初心者ユーザを一層混乱させる原因となってしまっています。下表に両者の違いを列記しましたので、まず両者が違う概念であることをしっかり認識して下さい。

　量子化学に関する日本語の文章内では、単に「Opt」「Optimization」という言葉が用いられた場合、構造最適化のことを指すことが多いですが、英語の文章内や、日本語でも文脈によってはSCF手続きにおけるエネルギーや軌道の最適化を指すこともありますので、文献等を読む場合にはご注意下さい。
　またこれに関連して、GaussianにはStableあるいはStable=Optというキーワードが用意されていますが、これらは分子軌道の最適化（SCF繰り返し手続き）に関するキーワードであり、分子構造の最適化とは無関係ですので、混同しないよう、併せてご注意下さい。

（4-付録）　HFおよびDFTエネルギー計算の理論的背景

　最後に付録として、HF/DFT計算のエネルギーや分子軌道を求めるための理論的背景をごく簡単に概説します。これにより第２部の配信内容の理解をより深めることができますが、あくまで付録ですので、興味のない方はこれ以降の部分を読み飛ばしていただいて構いません。また本メールニュースでは分かり易さを優先し、厳密性は度外視しておりますので、厳密な議論やより詳細な内容を知りたい場合は、一般的な量子化学の教科書をご参照ください^✝。（後の配信内容についても同様です。）
　HF計算、DFT計算において解くべき方程式は、それぞれHartree-Fock方程式、Kohn-Sham方程式と呼ばれますが、この２つの方程式は類似しており、Fock演算子 ƒ を用いて、以下のように共通の形で書くことができます。（ ƒ の中身がHFとDFTで若干異なることになります。）

ここで ψ_i と ε_i は、求めるべき分子軌道（molecular orbital; MO）とその軌道エネルギーです。また、r は電子の座標ベクトル、i はMO番号のindexを表します。残念ながらほとんどの場合、方程式(4.2)を直接解くのは困難なので、分子軌道は有限個の基底関数と呼ばれる既知関数の線形結合で記述できるという近似を施します。

ここで φ_μ は基底関数、C_μi は分子軌道係数です。この近似を施すと、φ_μ は既知であるため、求めるべきものは{C_μi}の組だけとなり、現実的な時間で方程式(4.2)を解くことができます。量子化学計算の場合、この基底関数は分子を構成する原子上に置かれることが多いため、φ_μ は基底関数と同義の言葉として、しばしば原子軌道（atomic orbital; AO）とも呼ばれます。そのため、式(4.3)の近似をlinear combination of atomic orbitals（LCAO）近似といいます。以降、μ などのギリシャ文字indexは、基底関数（あるいはAO）の番号を表すものとします。
　さて、式(4.3)を(4.2)に代入し、さらに式変形を続けると、最終的に以下の方程式が得られます。これは式(4.1)の等価表現であり、Roothaan方程式そのものです。

ここで、(4-2)節でも触れました通り、Fock行列 F と重なり行列 S がこの方程式のインプットパラメータであり、それらの行列要素はそれぞれ以下のように与えられます。

ただし

を表します。ここで、n_i は i 番目のMOの占有電子数を表し、閉殻分子の場合なら占有軌道で２、非占有軌道で０となるパラメータです。また、θ と h(r) は既知のパラメータと関数であり、HFかDFTかで中身が異なります。
　すると、式(4.5)、(4.6)において、軌道係数行列 C 以外の項はすべて既知、すなわちRoothaan方程式を解く前に用意できる量であることに注意して下さい。これらの既知の量をあらかじめ用意するプロセスが、(4-2)節、(4-3)節の図における「Fock行列を作るのに必要な項の計算」に相当します。また、式(4.5)の C_λi , C_κi は既知ではないので、それらの初期値は別途与えてやる必要があります。このプロセスが同図における「初期軌道（initial guess）の生成」に相当します。（仮の）軌道係数行列 C が決まればFock行列(4.5)が確定しますので、それを用いて方程式(4.4)を解くことで新たな C が得られます。それを式(4.5)に代入し、再び方程式(4.4)を解くと、また新たな C が得られます。この操作を繰り返すことにより、C がもはや変わらなくなるまで更新されていきますが、この更新プロセスが図中の「Roothaan方程式の繰り返し（SCF）計算」となります。
　SCFの手続きが収束し、C が得られれば、分子の全エネルギーは以下のように与えられます。

ここで、第１項はRoothaan方程式を解くことで得られる「電子の全エネルギー」、第２項は原子核同士のCoulomb反発に由来する「核の全エネルギー」です。第２項は原子核の座標{R_Α}と電荷{Z_Α}（すなわち、分子構造）が与えられた瞬間に決定される定数であり、したがって、SCF収束時には右辺は全て既知の量となります。分子の構造最適化を行う場合は、各原子（核）に働く力を計算するため、式(4.9)を各核座標で微分した表現を得る必要がありますが、その議論については次回配信の付録にて解説する予定です。
　ちなみに、「Fock行列を作るのに必要な項の計算」の中身をもう少し詳しく見てみると、それは基底関数の組{φ_μ}の生成と、式(4.6)～(4.8)の積分計算であることがわかります。これらの積分計算のうち、式(4.6)、(4.7)は１個の電子の座標にのみ依存する関数の積分であり、「一電子積分（one-electron integral）」と呼ばれます。一方、式(4.8)は２個の電子の座標に依存する関数の積分であり、「二電子積分（two-electron integral）」と呼ばれます。一般に、一電子積分の計算コストはたかだか基底関数の数の２乗であるため、相当大規模な分子でもほとんど一瞬で終わると考えて差し支えありません。一方、二電子積分のコストは大雑把には基底関数の数の４乗で推移するため、この二電子積分の計算がHF/DFT計算でのボトルネックとなっています。

✝ 例えば以下の教科書では、HF方程式の導出からRoothaan方程式やその解に至る過程が詳細に解説されています。
　 A. Szabo, N. S. Ostlund・著／大野公男, 阪井健男, 望月祐志・訳 「新しい量子化学(上)」 東京大学出版会

　今回の内容は以上です。次回（第５回配信）では、「Gaussian計算の流れ」を解説いたします。

メールニュース会員募集中！

Gaussian入門者の皆様に、Gaussianを使いこなして高度な計算化学者に飛躍していただけるよう、Gaussianに関する様々な情報を発信しております。メールニュースの配信をご希望の方は、以下のフォームよりお願いいたします（お問い合わせ内容の項に「Gaussian入門メールニュース配信希望」とご記入ください）。

メールにてお申し込みされる方は、以下の必要事項をご記入の上、送信してください。

• ◆電子メール件名 : Gaussian入門メールニュース配信希望
• ◆記入項目：
  1. 氏名 :
  2. E-mail：
  3. 法人名/部署名：
  4. 住所：
  5. 電話番号：